Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 20

000, 010, 111;

, , ;

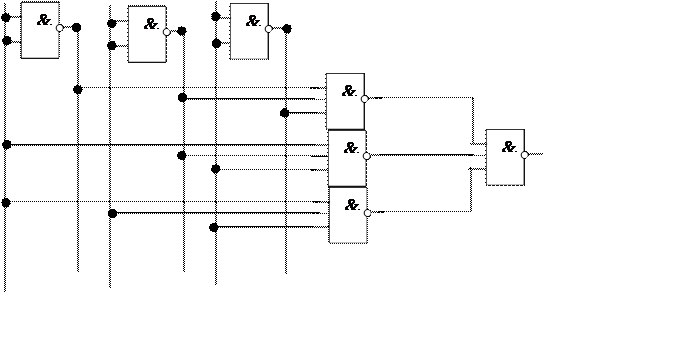
Минимизация булевых функций.

Одну и ту же булеву функцию можно представить в виде различных логических выражений тождественных друг другу. Практический интерес имеют выражения, содержащие наименьшее число букв, т. к. они позволяют упростить устройство, реализующее эту функцию. Такие функции называют минимальными. Поскольку в настоящее время используются три базиса: булев, Пирса и Шеффера, то будем изучать методы минимизации функций в булевом базисе, когда уравнения представляются в минимальных дизъюнктивных нормальных формах (МДНФ); в булевом базисе, когда уравнения записываются в минимальных конъюнктивных нормальных формах (МКНФ); в базисе Пирса и базисе Шеффера.

Проблеме минимизации посвящено огромное число работ, известно большое число различных методов минимизации. При небольшом числе аргументов булевой функции используют диаграммы Вейча (карты Карно). Метод чрезвычайно удобен при числе аргументов не более пяти. Диаграммы Вейча – это графическое представление таблиц истинности, когда таблица размещается на торе, естественно, что при использовании таблицы используют развертку тора. При выполнении заданных формальных правил «автоматически» производится выполнение операций склеивания и поглощения, а результатом будет минимальная форма булевой функции.

В литературе описаны методы получения МДНФ и МКНФ. При необходимости получения минимальных форм в базисе Пирса или Шеффера используют тождественные преобразования МДНФ или МКНФ. Такой подход вряд ли можно считать оправданным, т.к. минимальные формы функции в базисах Пирса и Шеффера можно легко получить по тем же самым диаграммам Вейча.  

Получение минимальных дизъюнктивных нормальных форм с помощью диаграмм Вейча.

При использовании диаграмм Вейча строится прямоугольная таблица (развертка тора), число клеток которой равно числу возможных наборов аргументов. Каждой клетке этой таблицы соответствует набор аргументов и конституента единицы равная единице на этом наборе. Требуется, чтобы  в соседних клетках эти конституенты отличались только одним сомножителем.

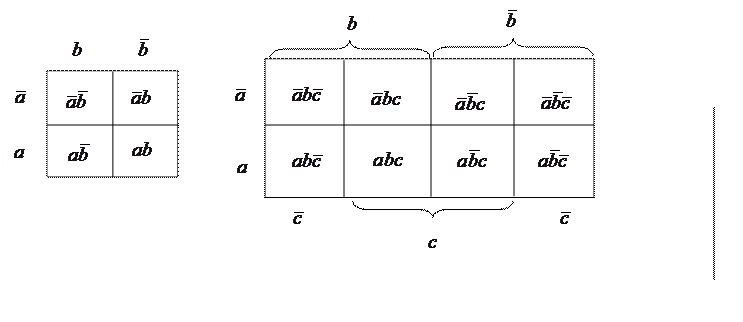
Диаграммы Вейча для функции 2 и 3 аргументов соответственно.

Для правильной разметки достаточно отводить половину таблицы под аргумент, а другую половину таблицы – под инверсию аргумента, при этом скобки на противоположных сторонах таблицы не должны совпадать!  Естественно, что возможно несколько вариантов разметки одной и той же таблицы.

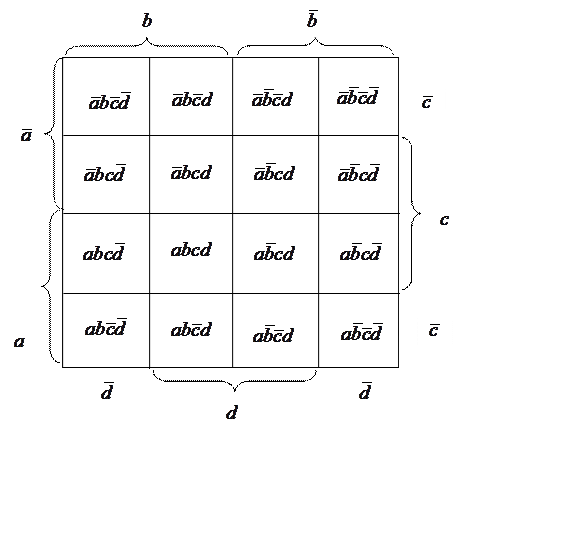Диаграмма Вейча для функции четырех аргументов.

Все клетки, которые отличаются значением только одной переменной, являются соседними. Для функции пяти и более переменных эти клетки могут быть расположены не рядом. Пример: клетке 3 соответствует конституента 1 . Клеткам 2, 4, 6, 27 – конституенты единицы , , , . Все эти клетки соседние для клетки 3.

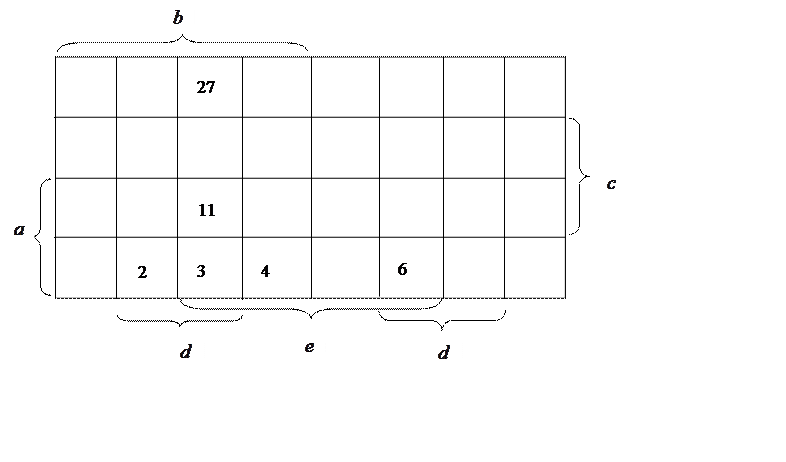
При минимизации следует руководствоваться следующими правилами:

1) Строится и размечается прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов.

2) В клетки таблицы заносятся значения булевой функции. При поиске клеточки таблицы аргумент набора равный 1 берется без отрицания, а равный нулю – с отрицанием. В найденную клетку записывают значение функции.

3) Обводят контурами все 1 с соблюдением следующих правил:

- контур должен быть прямоугольным;

- внутри контура не должно быть нулей;

- при обводке следует получить минимальное число контуров максимальной площади;

- число единиц в контуре должно быть равно степени числа 2 (1, 2, 4, 8, 16,…);

- одна и та же клетка, заполненная единицей может входить в несколько контуров;

- при обводке следует учитывать, что самая верхняя и самая нижняя строки таблицы являются соседними. Соседними являются также крайний левый и крайний правый столбцы.

- количество контуров должно быть как можно меньше, а площадь контуров – как можно больше.