Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 19

Заметим, что булев базис не является минимальным, т.к. из него можно удалить либо функцию И, либо функцию ИЛИ.

Аналитическая запись булевых функций в базисе Пирса.

Будем использовать следующее обозначение:

.

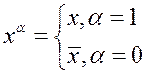Вспомним запись булевой функции в совершенной дизъюнктивной нормальной форме: . Символ  означает, что дизъюнкция берется только для таких наборов  на которых функция равна единице: . Попробуем записать эту функцию таким образом, чтобы оно содержало только функции Пирса и отрицания (отрицание также реализуется функцией Пирса: ). Просуммируем конституенты единицы наборов, где функция равно нулю. Мы получили новую функцию, значения которой противоположны исходной  функции, поэтому: 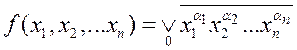.  Но последнее выражение есть не что иное, как функция Пирса: 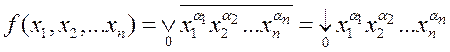 .  Однако конституенты единицы представляют собой конъюнкции переменных и от конъюнкций нужно также избавиться. Для этого преобразуем конституенты единицы: .

Таким образом, алгоритм перехода от табличного задания функции к аналитической записи в базисе Пирса таков:

1) выбрать в таблице все наборы аргументов, на которых функция равна нулю;

2) аргументы каждого из этих наборов объединяются функцией Пирса. Причем, если аргумент равен 1, то он записывается с отрицанием; если – 0, то без отрицания;

3) все полученные составляющие (термы) объединяются функцией Пирса.

Пример:

Выбираем наборы 010, 101, 111;

, , ;

3) .

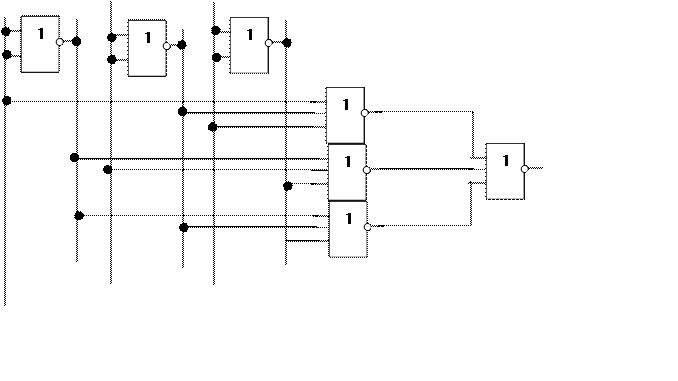
По аналитической записи функции можно нарисовать схему её реализующую:

Запись функций в базисе Шеффера.

Конституента нуля для набора  записывается так:

. Действительно, в силу определения конституенты нуля она равна нулю на этом наборе, следовательно все слагаемые в конституенте должны быть равны нулю. Отсюда следует правило, если в наборе аргумент равен единице, то в конституенту нуля он записывается с отрицанием, если нулю – без отрицания.

Известно, что любую функцию можно записать в совершенной конъюнктивной нормальной форме в виде произведения конституент нуля. Однако ее можно записать и  как инверсию функции  значения которой противоположны исходной функции:

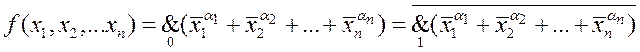
Символы  () обозначают,  что конъюнкциями связываются конституенты нуля наборов на которых исходная функция равна нулю (единице). Действительно, если на наборе  функция  равна единице, то можно указать для этого набора конституенту нуля равную нулю на этом наборе и единице – на остальных наборах. Конъюнкция этих конституент представляет собой новую функцию   равную нулю на тех наборах, где функция  равна единице, т.е.  и 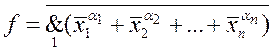. Полученное выражение – это функция Шеффера над конституентами нуля: . Для получения окончательной записи функции преобразуем конституенты нуля:

 Окончательное представление функции: . Следовательно, алгоритм перехода от таблицы истинности к аналитической записи в базисе Шеффера таков:

Выбрать в таблице все наборы аргументов на которых  функция равна единице;

Аргументы каждого из этих наборов связать операцией Шеффера, причем, если аргумент равен 1, то он записывается без отрицания, если нулю – с отрицанием.

Все полученные выражения также связываются операцией Шеффера.

Пример: