Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 10

2                          2

         1        

Найдем минимальные пути между всеми парами вершин графа:

		2	3	4	4	1
2		0	5	3	3	2
3		1	0	4	4	3
4		3	2	0	4	3
4		5	4	2	0	5
1		6	5	3	1	0

Определяем внешние передаточные числа вершин:

,

,

,  

,

.

Поскольку  - наименьшее число, то вершина  является внешней медианой графа.

Определяем внутренние передаточные числа вершин:

,

,

, 

,

.

Наименьшее число , поэтому внутренней медианой графа будет вершина . Вершина  имеет минимальное значение суммы внешнего и внутреннего передаточных чисел , следовательно, она является медианой.

Транспортной сетью называется граф без петель у которого

- существует единственная вершина , называемая истоком из которой дуги только выходят (входящих нет);

- существует единственная вершина , называемая стоком в которую дуги только входят;

- каждой дуге графа поставлено в соответствие целое число , называемое пропускной способностью дуги.

Обозначим:

-  -множество дуг выходящих из вершины  (для стока );

-  -множество дуг входящих в вершину  (для истока ).

Потоком по транспортной сети называется функция  определенная на всем множестве дуг графа, удовлетворяющая условиям

1.  для любой дуги графа справедливо  неравенство   ;

2. для всех дуг графа не являющихся истоком и стоком выполняется равенство    .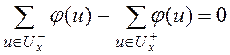                                                                                                                           

Из второго условия следует, что поток,  выходящий из истока равен потоку, входящему в сток: 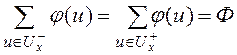. Величина  называется величиной потока транспортной сети.

Для исследования распределения потока по транспортной сети вводят понятие разреза транспортной сети. Пусть  множество вершин не содержащих истока, но содержащие сток. Полную совокупность дуг, заходящих в  и выходящих из   называют разрезом транспортной сети.

Т.к. в разрез всегда входит в сток, то величина потока, протекающего через разрез равна величине потока транспортной сети.

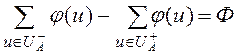, где  и  -множества дуг заходящих в  и выходящих из  .

Пропускной способностью разреза   называют сумму пропускных способностей дуг, заходящих в этот разрез:

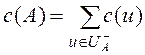
Поток по дуге не может превышать пропускной способности дуги: , а отсюда вытекает, что поток транспортной сети не может превысить пропускной способности разреза :

.

Дуга  называется насыщенной, если поток по дуге  равен пропускной способности этой дуги .

Поток  называют полным, если любой путь из  в содержит хотя бы одну насыщенную дугу.

Обратите внимание, что полный поток в транспортной сети не является константой. Если изменить направление потоков в некоторых дугах, то может измениться и значение полного потока.

Если транспортная сеть и пропускные способности  дуг известны, то естественна постановка задачи о наибольшем потоке,  когда требуется найти максимальную величину потока, которую может пропустить транспортная сеть и найти распределение этого потока по дугам  этой транспортной сети.

Известен алгоритм Форда-Фалкерсона,  позволяющий решать подобные задачи. Нахождение наибольшего потока производится в два этапа.

1.  Нахождение полного потока .

2.  Пошаговое увеличение потока  до тех пор, пока он не станет наибольшим.

Этап 1. Нахождение полного потока.

Выбираем любой путь из  истока  к стоку  содержащий только ненасыщенные дуги. Для каждой дуги этого пути подсчитываем разность между пропускной способностью дуги и потоком в этой дуге: . Выбираем минимальное значение  и увеличиваем поток во всех дугах пути на эту величину. При этом дуга с минимальным значением   становится насыщенной и увеличить поток по данному пути уже невозможно.