Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 4

Отношение называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично и транзитивно.

Пример: отношения «больше или равно», «меньше или равно».

Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно.

Пример: отношения «больше», «меньше», «раньше», «позже».

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ

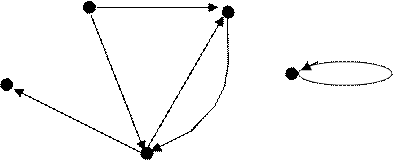
При решении задач в самых различных областях приходится изучать связи между объектами. Объекты помечаются точками, а связи между объектами –  линиями. Такой рисунок и  будет графом.  

                                   b

c

a                                                    e

d

Граф – это один из способов задания бинарных отношений. Пусть имеется некоторое множество , на котором задано бинарное отношение .  Из соотношения ,    следует 

. Если теперь каждый элемент из множества  изобразить точкой на плоскости, а все пары , для которых справедливо отношение  соединить ориентированными линиями (дугами), то получим представление бинарного отношения в форме графа.

Граф, показанный на рисунке,  имеет множество вершин ,  а отображение  определяет множество направленных дуг . . Стрелка на дуге направлена от первого элемента пары ко второму. Графы, вершины которых соединяются дугами, называются ориентированными графами или орграфами.

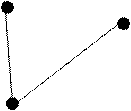
Часто в графах пару дуг противоположного направления соединяющих одну и ту же пару вершин заменяют неориентированной линией, называемой ребром. Если в графе вершины связаны  только ребрами, то  такой граф называют неориентированным или неографом.

                                         a

c        

b

Здесь множество вершин , .

Различные вершины называются смежными, если они соединены ребром или дугой.

Различные дуги или ребра называются смежными, если они имеют общую концевую вершину.

Дуга и вершина инцидентны, если вершина является для дуги концевой вершиной.

Способы задания графов

- аналитический (бинарным отношением);

- графический;

- матричный.

При матричном задании графов строится квадратная матрица, число строк и столбцов которой равно числу вершин графа

				…
…

Если в графе есть пара , то в матрицей будет соответствовать 1 в  строке и  столбце. Если же такой пары нет, то в эту клеточку записывают 0.

Полученная матрица называется матрицей смежности графов.

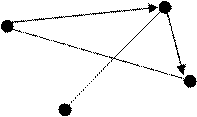
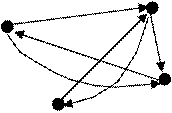
Пример:       

,     ,   

                               b                                                                     b

a                                                                   a

=

d                                                                         d

c                                                                    c

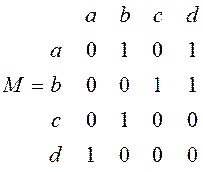
Типы графов       

Если изменить ориентацию всех дуг графа, то полученный граф называется обратным.

Вершина графа называется изолированной, если она не инцидентна ни одной из дуг.

Нуль  граф – граф состоящий из изолированных вершин.

Дуга для которой концевые вершины совпадают, называется петлей.

Граф называется полным, если для любой пары вершин и  существует дуга.

Если какие-то две вершины графа соединены несколькими дугами, то такой граф называют мультиграфом.

Во  многих случаях на графе отражают дополнительную информацию о вершинах и ребрах, например, о пропускной способности,  о расстоянии между пунктами и т. д. Если ,  - множества меток, то разметкой графа  называется пара функций  и . В этом случае вершина  помечается элементом , называемым весом вершины, а ребро    - элементом   -вес ребра. Часто бывают помеченными только вершины или только ребра. Граф с нагруженными ребрами – это граф с размеченными ребрами. Матрица смежности графа с нагруженными ребрами составлена из весов соответствующих ребер.