Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 25

 - не подходит, поскольку оно равно 1 не только на 0100 матрицы единиц, но и на наборах 0101, 0110, 0111 матрицы нулей;

 - не подходит, поскольку равно 1 на всех наборах матрицы нулей;

 -не подходит, т.к. равно 1 на наборах 0101, 1101 матрицы нулей;

 - не подходит, т.к. равно 1 на наборе 0110;

 -не подходит,  т.к. равно 1 на наборе 0101, 0110, 0111;

 - не подходит, т.к. равно 1 на наборе 0101;

 - не подходит, т.к. равно 1 на наборе 0110;

- не подходит, т.к. равно 1 на наборах 0101 и 1101;

- не подходит, т.к. равно 1 на наборе 0110;

 -подходит, поскольку не равно 1 ни на одном наборе матрицы нулей и покрывает наборы 0100, 0000 матрицы единиц.

Вписываем  в МДНФ и удаляем наборы 0100 и 0000 из матрицы единиц:

,

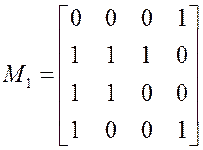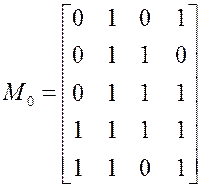
Выписываем набор 0001 матрицы единиц и аналогично ищем кратчайшее произведение равное единице на этом наборе:

 - не подходит, поскольку дает значение 1 наборам 0101, 0110, 0111 матрицы нулей;

 -подходит, поскольку не равно 1 ни на одном наборе матрицы нулей и покрывает наборы 0001, 1001 матрицы единиц. Вписываем  в МДНФ и удаляем наборы 0001 и 1001 в матрице единиц: ,

, .

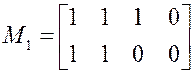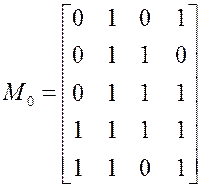Выписываем набор 1110 и, поочередно рассматривая претенденты , находим кратчайшее произведение  равное 1 на наборах 1110 и 1100 и равное нулю на всех наборах матрицы нулей. Вычеркиваем наборы 1110 и 1100 из матрицы единиц. Поскольку матрица единиц пуста – минимизация закончена. МДНФ имеет вид: .

Замечание: если искать покрытие матрицы единиц функцией Шеффера с минимальным числом аргументов, то получим минимальную форму в базисе Шеффера. Естественно, что следует учитывать особенности этой функции:

- если претендент, покрывающий набор матрицы единиц и равный нулю на всех наборах матрицы нулей состоит из одного аргумента, он должен записываться в минимальную форму с дополнительным отрицанием;

- если претендент покрывает все наборы матрицы единиц и равен нулю на всех наборах матрицы нулей, то он записывается с общим отрицанием. Для рассмотренного примера претенденты, которые входят в минимальную форму: , , , а минимальное выражение

Видно, что при работе алгоритма многократно проверяются уже отвергнутые претенденты, что сильно увеличивает время, затрачиваемое  на минимизацию. Рассмотрим модификацию алгоритма свободного от этого недостатка на примере получения МДНФ.

Рассматривается матрица нулей и формируется очередь допустимых претендентов, описываемых одним аргументом. Допустимым будет претендент, который равен нулю на всех наборах матрицы нулей. Если допустимый претендент покрывает хотя бы один набор матрицы единиц, он вписывается в формулу, а покрываемые наборы исключаются из матрицы единиц. Если – нет, то претендент в формулу не входит и рассматривается следующий  допустимый претендент из очереди. Если все наборы матрицы единиц удалены, работа алгоритма закончена, если же нет, рассматривается следующий допустимый претендент из очереди, а если очередь пуста, то формируется новая очередь допустимых претендентов, зависящих уже от двух аргументов и т.д.

Алгоритм получения МДНФ:

1) Задать длину претендента ;

2) Рассматривая матрицу нулей сформировать очередь всех допустимых претендентов длины ;

3) Если очередь пуста, принять  и перейти к пункту 2, иначе – к пункту 4;

4) Взять первого допустимого претендента из очереди и проверить покрывает ли он хотя бы один набор в матрице единиц. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5.

5) Включить допустимый претендент в формулу, представляющую собой сумму претендентов;

6) Исключить наборы, покрываемые претендентом из матрицы единиц;

7) Исключить претендент из очереди;

8) Если матрица единиц не пуста, то перейти к пункту 3, иначе – конец.

В рассматриваемом примере претенденты  недопустимы, поскольку обращают в единицу один или несколько наборов  матрицы нулей.