Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 7

В результате получено 3 связных подграфа (или  3 компоненты связности):

a                  d                  b         c   

e                                       f                     h                     g

Ориентированный граф называется связным, если любые его две вершины, соединены по крайней мере одним путем.

Ориентированный граф называется сильно  связным, если любые две его вершины  и  соединены по крайней мере одним направленным путем  с началом в  и по крайней мере одним направленным путем  с началом в .

Пусть  и  -матрицы достижимостей и контрадостижимостей графа

. Две вершины графа    и  называют взаимодостижимыми, если . Отношение взаимодостижимости может быть выражено матрицей  элементы которой , если вершины  и  взаимодостижимы. Отношение взаимодостижимости рефлексивно, симметрично и транзитивно, следовательно оно является отношением эквивалентности и разбивает множество вершин графа  на классы взаимодостижимых вершин. Каждый такой подкласс порождает подграф, который называется максимально сильно связанным подграфом графа .

Пример: разложить граф  на максимально сильно связанные подграфы.

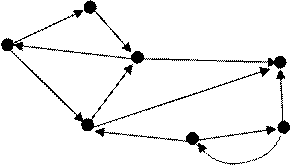                                           x3

x1                           x2                    x7

x4                                       x5

x6

Матрицы достижимостей, контрадостижимостей и взаимодостижимосей имеют вид:

D=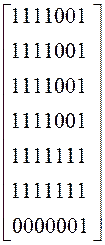,  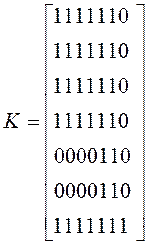 и .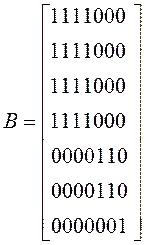

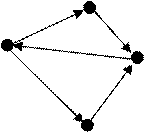
Из матрицы взаимодостижимости легко находятся множества взаимодостижимых вершин ,  , . Зная эти множества можно начертить три максимально сильно связанных подграфа графа :

       x1                        x2                x6                    x5                         x7

x4

Пусть  - неориентированный граф. Количество ребер, инцидентных вершине  называется локальной степенью вершины или просто степенью.

Локальную степень вершины   графа можно вычислить по матрице смежности путем суммирования  элементов  столбца. Действительно, в  столбце, соответствующем вершине  единицы стоят на пересечении со строками, которым соответствуют инцидентные этой вершине ребра, а остальные элементы столбца равны нулю.

Теорема: Сумма локальных степеней графа всегда четная.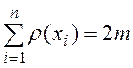, где - число вершин, - число ребер.

Доказательство: т.к. каждое ребро вносит в общую сумму степеней всех вершин число 2, то сумма должна быть равна удвоенному числу ребер.

Теорема: В любом графе количество вершин нечетной степени четно.

Доказательство: Сумма локальных степеней графа равна . Сумма степеней вершин с четными степенями четна. Если от четного числа  отнять  это четное число, то мы получим также четное число, которое равно сумме степеней вершин с нечетными номерами. При суммировании нечетных чисел сумма может быть четной только при четном числе слагаемых. 

Для вершин ориентированного графа существуют две локальные степени:  - количество выходящих  из вершины дуг,  - количество входящих в вершину  дуг. Петля дает вклад 1 в обе степени.

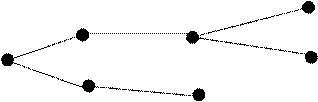          Неориентированный граф называется деревом, если он связен и не имеет циклов.

Рассмотрим дерево с  вершинами и  ребрами. Можно сформулировать следующие основные свойства деревьев:

- Каждая пара вершин дерева связана единственной цепью. (Если допустить существование двух цепей, то они образуют цикл, что противоречит определению дерева).

- Дерево это связный граф, но при удалении ребра связность нарушается.

- Число ребер на единицу меньше числа вершин:  (При удалении ребра из дерева,  число деревьев увеличивается на единицу). При удалении следующих ребер, число полученных деревьев будет на единицу больше, чем число удаленных ребер. После удаления всех ребер останутся только изолированные вершины,  число которых на единицу больше, чем число удаленных ребер).

- Дерево ациклично, но при добавлении хотя бы одного ребра появляется цикл.

В любом связном графе есть подграф, являющийся деревом и включающий в себя все вершины графа. Такой подграф называется покрывающим деревом или каркасом.