Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 33

Рассмотрим, например, заполнение клеточки для случая, когда автомат находится в состоянии  (код 01), а на вход приходит сигнал  (код 1). Согласно таблице переходов автомат должен переключиться в состояние  (код 00). Следовательно, первый триггер должен переключиться из  0 в 0, а второй триггер – из 0 в 1. Вспомните принцип работы Т-триггера: если на управляющий вход V подать 0, то триггер останется в том же состоянии, если же на вход V подать 1, то после прихода синхросигнала триггер переключится в противоположное состояние. Понятно, что для обеспечения требуемого переключения автомата на вход V первого триггера нужно подать 0, а на вход V второго триггера подать 1.

                       

                   

         

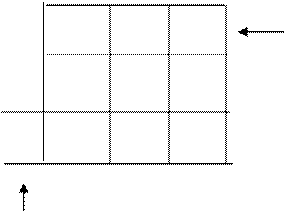
                                                 01      10      00                 A(t)

                   0                                              

                   1        01                         

 

                                                                                    

Z(t)      V1    V2

После заполнения таблица функций возбуждения элементов памяти имеет вид:

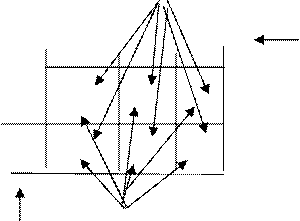                                 V₂

01      10      00                A(t)

0        00      10      10     

1        01      11      00

Z(t)          V₁

Эта таблица является таблица истинности комбинационной схемы 1.    

Запишем эту же таблицу в привычном виде:

Z	Q1	Q2	V1	V2
0	0	1	0	0
0	1	0	1	0
0	0	0	1	0
1	0	1	0	1
1	1	0	1	1
1	0	0	0	0

Минимизируем функции  и :

Таблица для V₁                        Таблица для V₂

 

                                                      

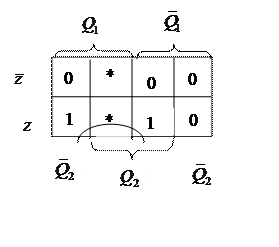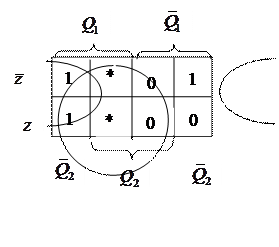Минимизированные функции:  и /

Зная структурную схему конечного автомата, по полученным уравнениям чертят функциональную схему конечного автомата.

                            Минимизация полностью определенных автоматов.

Определение. Два состояния автомата  и  называются эквивалентными, если реакция автомата, находящегося в состоянии  совпадает с реакцией конечного автомата, находящегося в состоянии  для слов произвольной длины.

Для минимизации числа состояний следует получить разбиение множества состояний конечного автомата на непересекающиеся подмножества эквивалентных состояний (классы эквивалентности). Если в каждом подмножестве оставить только одно состояние, то получится автомат с минимальным числом состояний. 

Определение. Два состояния автомата  и  называются k - эквивалентными, если реакция автомата, находящегося в состоянии  совпадает с реакцией конечного автомата, находящегося в состоянии  для слов длины k.

Алгоритм минимизации числа состояний:

Шаг 1. Находятся последовательные разбиения  множества состояний автомата на  классы одно -, двух -,…,  -,  - эквивалентных состояний. Шаг выполняется до тех пор, пока в каждом классе окажется только по одному состоянию, либо когда текущее разбиение не совпадет с предыдущим разбиением: . Нетрудно убедиться, что последующие разбиения будут также совпадать с, т.е. полученные  - эквивалентные состояния являются просто эквивалентными. 

Шаг 2. В каждом классе разбиения  оставляют по одному состоянию.

Шаг 3. В таблице переходов – выходов вычеркивают столбцы, соответствующие удаленным состояниям. Если в оставшихся столбцах имеются символы удаленных состояний, то они заменяются на не удаленные эквивалентные им состояния.

Шаг 4. В качестве начального состояния выбирается любое состояние эквивалентное