Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 21

4) Записывают минимальное выражение как дизъюнкцию логических  произведений, которые описывают контура таблицы. Для поиска логического выражения для контура выясняют от каких аргументов он зависит. Если все 1 контура приписаны к аргументу , то в логическое произведение этот аргумент входит. Если все единицы контура помечены инверсией аргумента, то в произведение вписывается . Если в контуре есть 1, помеченные   и 1, помеченные , то в описание контура этот аргумент не входит.

Минимизируемая функция должна быть задана таблицей, либо совершенной дизъюнктивной нормальной формой.   

Пример: Найти МДНФ функции

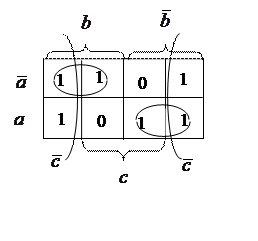В этом таблице три контура. Один из них «разрезан» при развертке тора. Минимальное выражение:

Пример: минимизировать не полностью определенную булеву функцию, заданную таблицей.

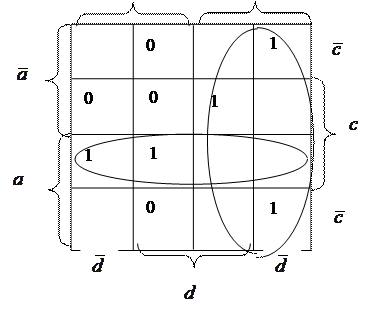В данном примере не полностью определенная функция была доопределена таким образом, чтобы получить минимальное число контуров максимальной площади, что обеспечивает наиболее простое логическое выражение функции. Естественно, что обведенные пустые клетки доопределены единицами, а не обведенные – нулями. Результат: .

В некоторых случаях МДНФ инверсной функции проще, чем МДНФ исходной функции. Пример:

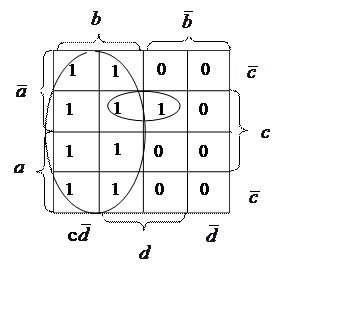
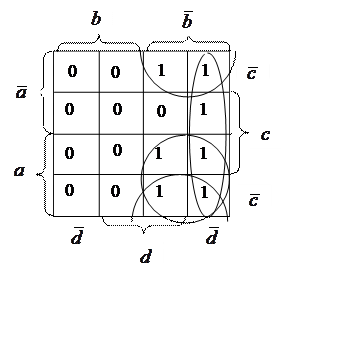
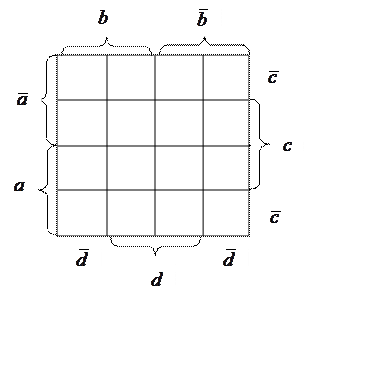
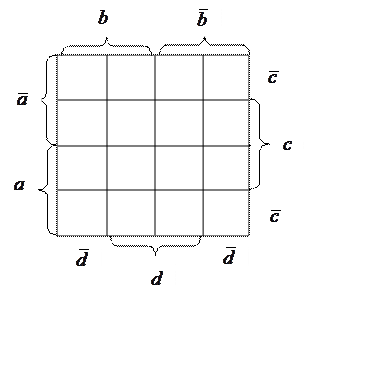
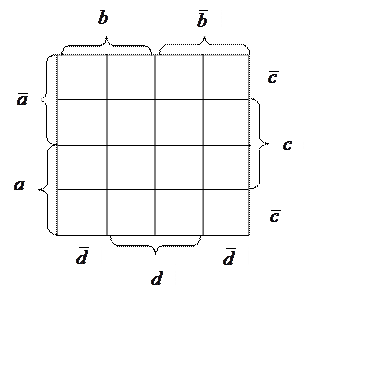
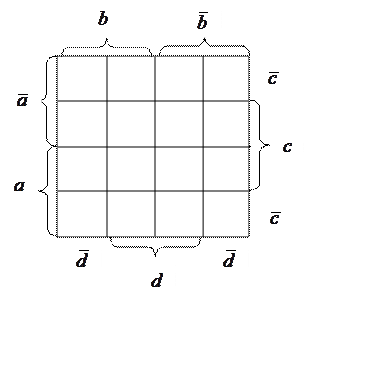
Минимизация булевых функции в базисе Шеффера.

Обычно, при необходимости получения минимального выражения в базисе Пирса или Шеффера функцию минимизируют в булевом базисе, а затем, используя правила де Моргана, преобразуют функцию.

Пример: запишем функции  и  в базисе Шеффера:

;

.

Однако, ранее рассмотренные свойства операций Шеффера и Пирса, похожие на операции склеивания и поглощения позволяют записывать минимальные формы функций в базисах Шеффера и Пирса используя диаграммы Вейча.

Минимизация булевых функции в базисе Шеффера с помощью диаграмм Вейча.

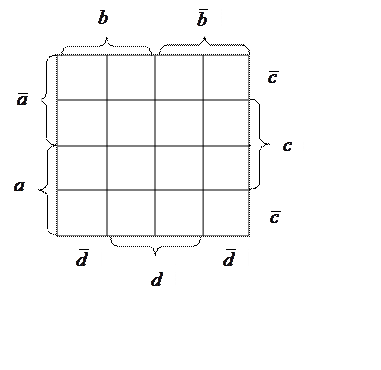
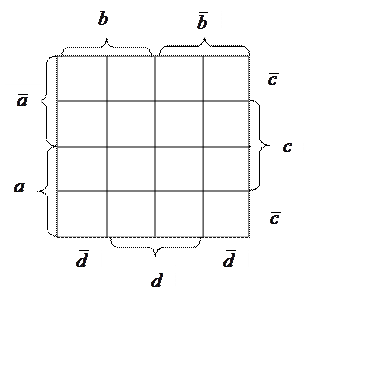
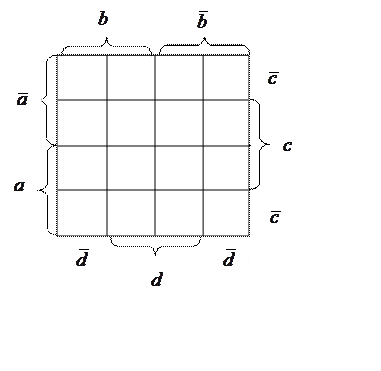
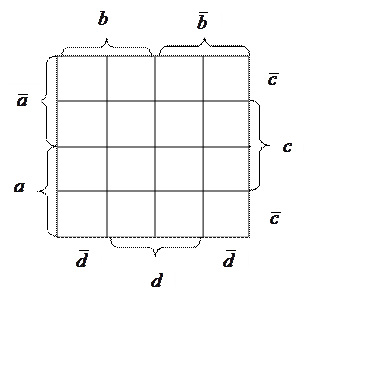
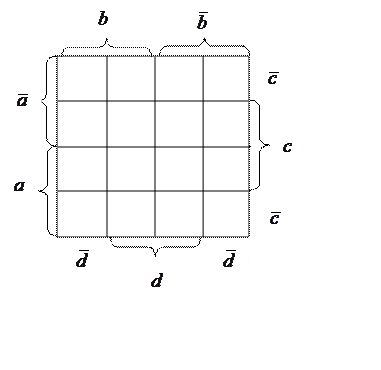
При использовании диаграмм Вейча строится прямоугольная таблица, число клеток которой равно числу возможных наборов аргументов. Каждой клетке этой таблицы соответствует набор аргументов и - местная функция Шеффера, где  - число аргументов функции, равная единице на этом наборе. Требуется, чтобы  в соседних клетках эти функции отличались только одним аргументом.

При минимизации следует руководствоваться следующими правилами: