Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 28

	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1
	0	1	1	0	1	0	0	1
	0	0	0	1	0	1	1	1

Минимизируем эти функции в базисе Шеффера (И-НЕ):

;

.

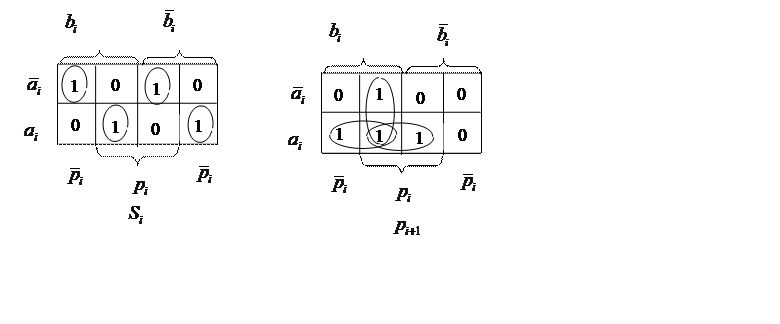
Достаточно часто при изображении схем используют так называемый жгут. Жгут – это изображение множества проводников одной жирной линией. Естественно, что провода входящие в жгут и выходящие из него должны маркироваться.

Изобразим функциональную схему одноразрядного сумматора:

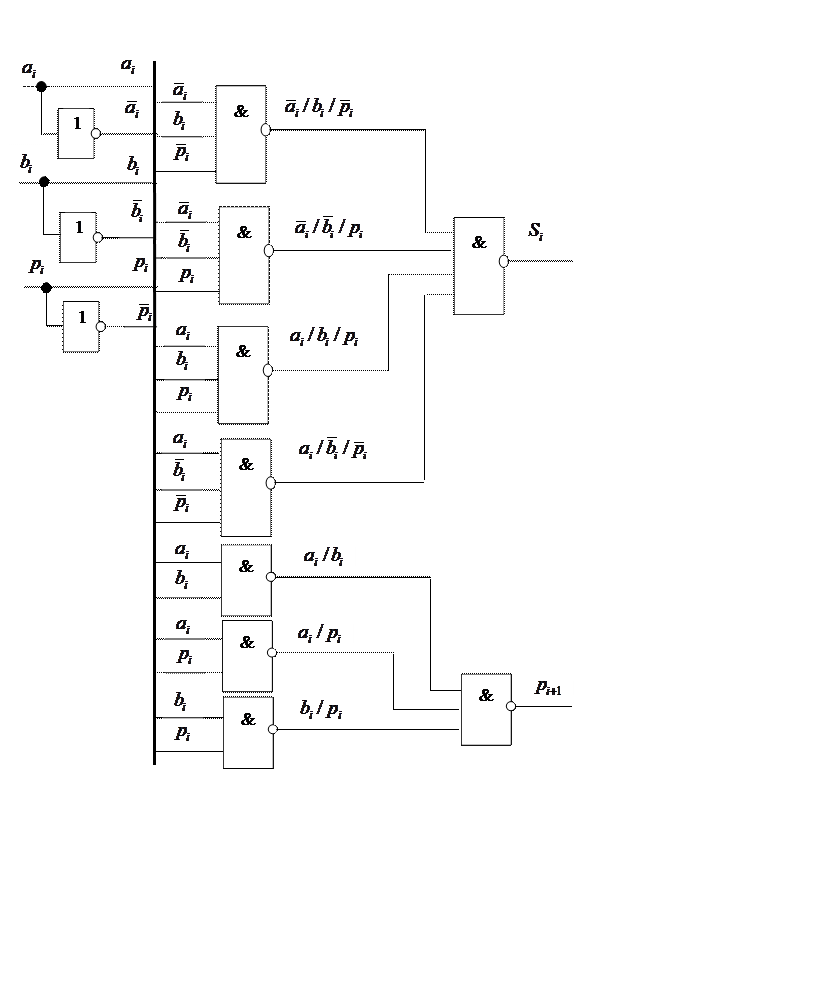
Самостоятельно получите минимальные выражения для этих функций в булевом базисе в дизъюнктивной форме, в булевом базисе в конъюнктивной форме, в базисе Пирса (ИЛИ-НЕ) и начертите схему сумматора в каждом из этих базисов.

                                Конечные автоматы.

Если выходные сигналы схемы в момент времени t зависят только от входных сигналов поступивших на схему в момент времени t то такая схема называется комбинационной схемой. Пример:

&

                        A(t)

1

                                                                    

    B(t)                                         Y(t)=A(t)*B(t)+C(t)

C(t)

В отличие от комбинационных схем у конечного автомата выходной сигнал схемы в момент времени t зависит не только от входных сигналов поступивших в момент времени t, но и от сигналов в предшествующие моменты времени. Предшествующие внешние воздействия запоминаются автоматом путем изменения его внутреннего состояния. Часть автомата, хранящую конкретное состояние называют внутренней памятью конечного автомата.

Основное качество, отличающее конечный  автомат от других устройств – наличие дискретного счетного множества внутренних состояний и свойство скачкообразного перехода из одного состояния в другое. Моменты перехода из одного состояния в другое определяются генератором синхроимпульсов. Изменение состояния происходит под действием входных сигналов, которые возникают вне автомата и поступают к нему по конечному числу входных каналов. Результатом работы автомата является выдача выходных сигналов во внешние цепи по конечному числу выходных каналов.

Общая теория конечных автоматов может быть разбита на две части:

-абстрактная теория,

-структурная теория.

В абстрактной теории рассматриваются вопросы функционирования конечного автомата. На этом этапе автомат рассматривают как черный ящик, внутренняя структура которого не известна.

В структурной теории рассматривается внутренняя структура конечного автомата.

                        Абстрактный конечный автомат

Абстрактный конечный автомат – это математическая модель автомата, задаваемая множеством из семи элементов: , где

 –множество внутренних состояний (алфавит состояний),

 – начальное состояние конечного автомата,

  – множество входных сигналов (входной алфавит),

 – множество выходных сигналов 1-го рода

(выходной алфавит 1-го рода),

  – множество выходных сигналов 2-го рода

(выходной алфавит 2-го рода),

  – функция переходов.

Функция переходов показывает, в какое состояние переключится автомат в следующий момент времени, если в данный момент времени автомат находился в состоянии , а на вход поступал сигнал : .

 – функция выходов 1-го рода которая показывает, какой выходной сигнал 1-го рода сформируется на выходе 1-го рода в данный момент времени, если в данный момент времени автомат находился в состоянии a(t), а на вход поступал сигнал z(t): .

   – функция выходов 2-го рода показывает, какой выходной сигнал 2-го рода сформируется на выходе 2-го рода в данный момент времени, если в данный момент времени автомат находился в состоянии , а на вход поступал сигнал :   .