Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 9

В ориентированном графе может существовать несколько путей  из      вершины  в вершину . Кратчайший путь – это путь с минимальной суммарной мерой,  соединяющий выбранные вершины. Существует много алгоритмов нахождения кратчайшего пути. Одним из эффективных алгоритмов является алгоритм Дейкстры. При использовании алгоритма последовательно помечают вершины, начиная от исходной. На каждом шаге к вершине приписывается число равное значению минимального пути от исходной вершины до рассматриваемой. После пометки конечной вершины работа алгоритма заканчивается. Если работу алгоритма заканчивать после отметки всех вершин, то будут найдены минимальные пути от выбранной начальной вершины графа до всех остальных вершин.

Пусть  и  начальная и конечная вершины;

 - число приписываемое вершине , равное значению минимального пути от начальной вершины ;

 -  значение пути из вершины  в смежную вершину ;

- число, приписываемое  к помечаемой вершине 

Шаг 1. Пометить начальную вершину  числом , а остальные вершины – символом ¥.

Шаг 2. Положить  (т.е. выбирается начальная вершина).

Шаг 3. Для всех неотмеченных вершин вычислить .

Шаг 4. Отметить вершину  с минимальным значением  и отметить дугу, выбранную на данном шаге.

Шаг 5. Положить .

Шаг 6. Если  , то переход к шагу 3, иначе конец. Найденный путь будет состоять из отмеченных дуг и будет минимальным.

Замечание: если шаг 6 модифицировать так, что переход к шагу 3 происходит, если не все вершины отмечены, иначе – конец,  то получим минимальные пути от выбранной начальной вершины до остальных вершин.

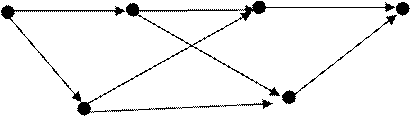
Пример: найдем минимальные пути в графе с использованием алгоритма Дейкстры. Вершина  - начальная.

               2             5                  1          

3            5                    4              5

                 4                             

Шаг 1. ,  для .

Шаг 2.   Выбрана начальная вершина .

Шаг 3.  - пометка для вершины ;

;

;

;

.

Шаг 4. Отмечаем вершину  и дугу  -нашли кратчайший путь от  к           .

Шаг 5.  - указана вершина .

Шаг 6. Т.к. не все вершины помечены, то переход к шагу 3.

Шаг 3. ;

;

;

.

Шаг 4. Отмечаем вершину  и дугу .

Шаг 5.  

Шаг 6. Т.к. не все вершины помечены, то переход к шагу 3.

Шаг 3.  ;

;

.

Шаг 4. Отмечаем вершину   и дугу .

Шаг 5. .

Шаг 6. Т.к. не все вершины помечены, то переход к шагу 3.

Шаг 3.  ;

.

Шаг 4. Отмечаем вершину  и дугу .

Шаг 5.  

Шаг 6. Т.к. не все вершины помечены, то переход к шагу 3.

Шаг 3.  .

Шаг 4. Отмечаем вершину   и дугу .

Шаг 5. .

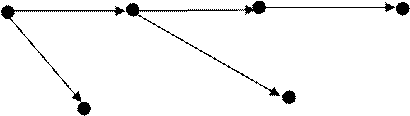
Шаг 6. Поскольку все вершины помечены, то конец.

Отмеченные вершины и дуги задают ориентированное дерево минимальных путей.

                                       

               2             5                  1          

3                                 4             

                                               

                            

Замечание: если при выполнении шага 3 все , то пути из  в

не существует.

Существует большое число задач, связанных с выбором наилучшего размещения в сети некоторых центров: складов в торговой сети, коммутационных узлов в сетях передачи информации и т.д. Решение подобных задач возможно при использовании понятия медианы графа.

Внешним передаточным числом вершины  называется сумма минимальных путей из вершины графа  в остальные вершины графа:

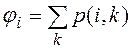
Внутренним передаточным числом называют сумму минимальных путей из всех вершин графа в вершину :   .

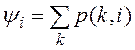Иногда, для учета «важности» пунктов рассматриваемой сети, каждой вершине приписывают определенный вес. Тогда формулы для передаточных чисел несколько изменяются: , .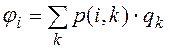

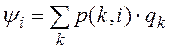Внешней медианой графа называется вершина с минимальным внешним передаточным числом. Внутренней медианой графа называется вершина с минимальным внутренним передаточным числом. Медианой графа называют вершину, для которой сумма внутреннего и внешнего передаточного чисел минимальна.

Пример: Найдем медиану указанного графа с весами вершин , , , ,  

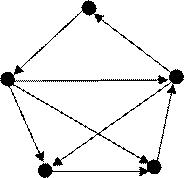                                     1                   2

                3               

3       3