Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 8

При построении каркаса берут ребро графа и добавляют другие ребра не создающие циклов до тех пор, пока нельзя будет добавить ни одного ребра из-за появляющегося цикла.

Граф может содержать несколько каркасов.

 

                                                                              

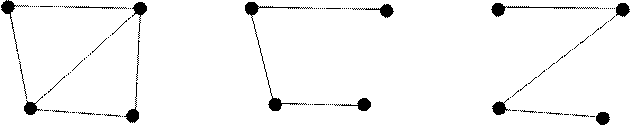 и  -каркасы графа

Оптимизация на графах

Существует большое число задач, связанных с решением оптимизационных задач на графах. Например: поиск кратчайшего или длиннейшего пути на карте между пунктами; нахождение сетей минимальной стоимости и т. д.  При решении подобных задач используют взвешенные графы , каждой вершине (ребру) которого приписывается некоторое число. Будем рассматривать графы, в которых число задается на ребрах графа.

Число  приписанное к некоторой дуге или ребру будем называть мерой  дуги или ребра . В зависимости от конкретной задачи  мера может иметь различный смысл: расстояние, стоимость и.т.д.

Мерой пути в графе будем называть сумму мер дуг, составляющих данный путь:

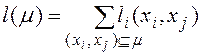
1.  Построение минимального каркаса.

Пусть задан неориентированный граф с нагруженными ребрами.

Требуется выбрать  ребра графа  таким образом, чтобы полученный подграф был каркасом графа с минимальной суммой мер ребер.

Простейшим алгоритмом решения служит алгоритм Краскала. При его выполнении составляется список ребер в порядке увеличения мер ребер. Дальнейшие шаги заключаются в выборе ребер начиная с ребра с минимальной мерой. Если очередное ребро приводит к образованию цикла, то его отбрасывают. Когда выбранное число ребер на единицу меньше числа вершин процесс прекращают.

Пример: требуется построить линию электропередач минимальной стоимости между населенными пунктами a,b,c,d,e,f. Стоимость линий между различными пунктами известна.

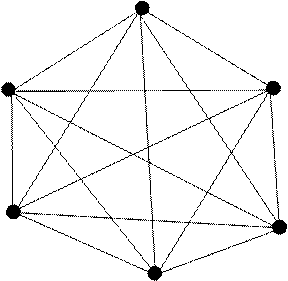                                              a

f                                                   b

e                                                     c

d

Стоимость строительства линий приведена в таблице:

	a	b	c	d	e	f
a	-	2	4	7	8	3
b		-	5	1	3	6
c			-	9	4	7
d				-	2	5
e					-	3
f						-

Составляем таблицу в порядке увеличения веса ребер:

Вес ребра	Ребра
1
2	,
3	,,
4	,
5	,
6
7	,
8
9

Поскольку у графа 6 вершин, то для построения каркаса нам нужно выбрать 5 ребер. Устанавливаем значение счетчика

Выбираем  - стоимость 1,  ;

Выбираем  - стоимость 2,  ;

Выбираем  - стоимость 2,  ;

Выбираем  - стоимость 3, ;

Выбираем  - стоимость 3, однако это ребро создает цикл и его следует отбросить,   ;

Выбираем  - стоимость 3, опять возникает цикл, поэтому и это ребро исключаем,  ;

Выбираем  - стоимость 4,  . Число выбранных ребер дерева на единицу меньше числа вершин графа, поэтому процесс завершен. Общая стоимость 12.

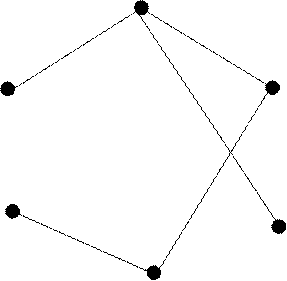                                              a

3                      2

f                                                   b

4

1

e                                                    c

2

d

Замечание: изученный алгоритм может применяться для нахождения максимального каркаса. Для этого на каждом шаге следует выбирать ребро с максимальной мерой.

2.  Нахождение минимального пути в ориентированном графе.