Используем матричный метод. Единичная матрица ![]() это матрица достижимостей с использованием
путей длины 0. Матрицу смежности
это матрица достижимостей с использованием
путей длины 0. Матрицу смежности ![]() задающую отношение
задающую отношение ![]() на множестве вершин
на множестве вершин ![]() можно интерпретировать как матрицу
достижимостей с использованием путей длины 1. Матрица
можно интерпретировать как матрицу
достижимостей с использованием путей длины 1. Матрица ![]() (транспонированная
матрица) задает обратное отношение
(транспонированная
матрица) задает обратное отношение ![]() и интерпретируется как
матрица контрдостижимостей с использованием путей длины 1. Матрицы
и интерпретируется как
матрица контрдостижимостей с использованием путей длины 1. Матрицы ![]() и
и ![]() - это
матрицы достижимостей и контрдостижимостей для путей длины 2 и т.д.
- это
матрицы достижимостей и контрдостижимостей для путей длины 2 и т.д.
Матрица достижимостей ![]() состоит
из элементов
состоит
из элементов ![]() .
.
![]() , если вершина
, если вершина ![]() достижима из
достижима из ![]() и
и ![]() в противном случае.
в противном случае.
Матрица контрдостижимостей ![]() состоит
из элементов
состоит
из элементов ![]() ,которые определяются следующим образом:
,которые определяются следующим образом: ![]() , если вершина
, если вершина ![]() достижима
из
достижима
из ![]() и
и ![]() в
противном случае.
в
противном случае.
Получить матрицу достижимостей можно, последовательно
объединяя матрицы ![]() . Процесс объединения
заканчивается, когда результат объединения перестает меняться.
. Процесс объединения
заканчивается, когда результат объединения перестает меняться.
Матрица контрдостижимостей может быть получена
транспонированием матрицы ![]() .
.
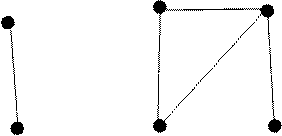
Пример: для графа, показанного на рисунке построить матрицу
достижимостей и контрдостижимостей , найти множества вершин достижимых и
контрадостижимых из ![]() .
.
a
e
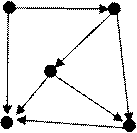
c d
Матрица смежности имеет вид: 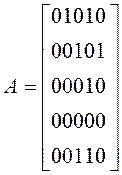
Находим ![]() :
:
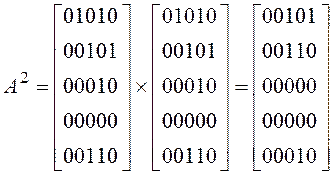
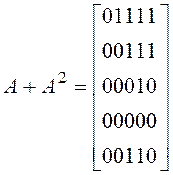
Поскольку ![]() следует искать
следует искать ![]() и вычислять
и вычислять ![]() :
:
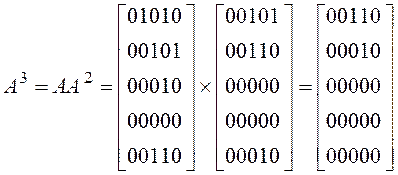 ,
,
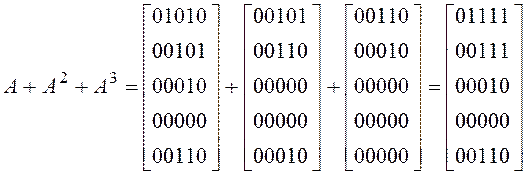 .
.
Т.к. ![]() , то процесс закончен,
и рассчитываем матрицу достижимостей:
, то процесс закончен,
и рассчитываем матрицу достижимостей:
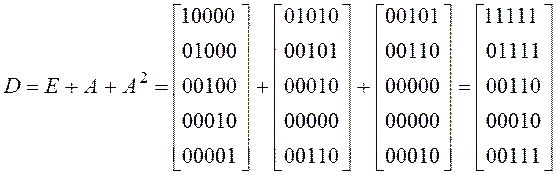 .
.
Матрицу контрдостижимостей находим путем транспонирования матрицы достижимостей:
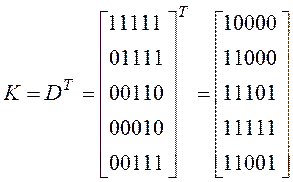 .
.
Для определения множества вершин достижимых из ![]() рассматриваем строку
рассматриваем строку ![]() матрицы
матрицы ![]() :
00111. Единичные элементы соответствуют вершинам, которые достигаются из
:
00111. Единичные элементы соответствуют вершинам, которые достигаются из ![]() :
: ![]() ,
, ![]() ,
, ![]() .
.
Для определения вершин из которых можно достигнуть ![]() выписываем строку
выписываем строку ![]() матрицы
контрдостижимостей 11001, которая и определяет множество искомых вершин
матрицы
контрдостижимостей 11001, которая и определяет множество искомых вершин ![]() .
.
Известен простой алгоритм определения матрицы
достижимостей ![]() :
:
Шаг 1. Задаем номер строки ![]() и
осуществляем переход к шагу 2.
и
осуществляем переход к шагу 2.
Шаг 2. Записываем ![]() строка
матрицы
строка
матрицы ![]() . В ней помечаем
единицей элементы, для которых существует путь из вершины
. В ней помечаем
единицей элементы, для которых существует путь из вершины ![]() длиной 1. (Это
длиной 1. (Это ![]() строка
матрицы смежности).
строка
матрицы смежности).
Шаг 3. Отмечаем элемент ![]() строки
матрицы
строки
матрицы ![]() равный 1, определяем
номер
равный 1, определяем
номер ![]() соответствующего ему столбца. Выбираем
соответствующего ему столбца. Выбираем ![]() строку матрицы смежности и дополняем
строку матрицы смежности и дополняем ![]() строку матрицы
строку матрицы ![]() единичными
элементами
единичными
элементами ![]() строки.
строки.
Шаг4. Если остаток ![]() строки
заполнен единицами, либо все 1 первой строки помечены, то переход к шагу 5.
Если же в первой строке есть еще неотмеченные элементы, то переходим к шагу 3.
строки
заполнен единицами, либо все 1 первой строки помечены, то переход к шагу 5.
Если же в первой строке есть еще неотмеченные элементы, то переходим к шагу 3.
Шаг 5. Если не все строки обработаны, то увеличиваем номер
строки ![]() на единицу и переходим к шагу 2, иначе –
шаг 6.
на единицу и переходим к шагу 2, иначе –
шаг 6.
Шаг 6. В полученной матрице элементы главной диагонали заполняются единицами.
Попробуйте проследить работу этого алгоритма для предыдущего примера.
Граф называется связным, если между его любыми вершинами имеется цепь.
 b c
b c
a
d e f
Этот граф не связный, т.к. нет некоторых цепей,
например из ![]() в
в ![]() , из
, из ![]() в
в ![]() и т. д.
и т. д.
Любой граф можно разбить на подграфы, каждый из которых является связным. Минимальное число таких подграфов, называется числом связности графа. Примером области применения этого понятия являются вычислительные сети.
Пусть граф задан множеством вершин ![]() и множеством ребер
и множеством ребер ![]() .
При определении связности можно воспользоваться следующим алгоритмом:
.
При определении связности можно воспользоваться следующим алгоритмом:
Шаг 1. Определить множество ![]() . Задать
значение коэффициенту связности
. Задать
значение коэффициенту связности ![]() .
.
Шаг 2. Взять вершину ![]() и найти
все вершины, соединенные цепью с
и найти
все вершины, соединенные цепью с ![]() .
.
Удалить найденные вершины из ![]() и
соответствующие ребра из
и
соответствующие ребра из ![]() . Увеличить
значение коэффициента связности
. Увеличить
значение коэффициента связности ![]() на единицу.
на единицу.
Шаг 3. Если ![]() , то перейти к шагу 2,
иначе – конец.
, то перейти к шагу 2,
иначе – конец.
Пример: a b c d
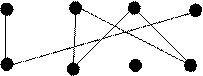 |
e f g h
Шаг 1. ![]() и
и ![]() ;
;
Шаг 2. Выбираем ![]() , после удаления
, после удаления ![]() и
и ![]() .
.
Шаг 3. Поскольку ![]() , то переход к шагу 2.
, то переход к шагу 2.
Шаг 2. Выбираем ![]() , после удаления
, после удаления ![]() и
и ![]() .
.
Шаг 3. Поскольку ![]() , то переход к шагу 2.
, то переход к шагу 2.
Шаг 2. Выбираем ![]() , после удаления
, после удаления ![]() и
и ![]() .
.
Шаг 3. Поскольку ![]() - пусто, то конец.
- пусто, то конец.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.