Теория множеств. Тождества алгебры множеств. Основные понятия теории графов. Методы задания конечных автоматов. Синтез функциональной схемы конечного автомата, страница 3

Бинарным  отношением  между множествами  и  называется произвольное подмножество прямого произведения множеств . Если , это записывают  и говорят, что  находится в отношении  к элементу . Бинарные отношения имеют наибольшее применение в теории информационных процессов

Если , то отношение есть подмножество и говорят просто об отношении  на  .

Пример

Пусть  -множество водителей, а  - множество автомашин, тогда .

Поскольку множество содержит шесть элементов, то существует  подмножеств множества  , т.е. существует 64 различных отношения на

.  Одно из них .

Пример:  - множество людей. Для этого множества могут быть определены отношения

- учится в одном университете;

- быть родственником и т.д. и т.п.

Итак, отношение  на множествах   есть множество пар, первые компоненты которых принадлежат , а вторые - . Множество  для такого отношения называется множеством отправления,  - множество прибытия.

Поскольку отношение – это множество, то для его задания можно использовать известные методы задания множеств. Для отношений на конечных множествах обычно используется матричный способ задания.

Пусть имеются множества  и  с мощностью  и .  Соответствие  можно задать с помощью матрицы  с размерностью .  При этом элементам множества   ставятся в соответствие строчки матрицы, а элементам множества  - столбцы матрицы. Если пара , то на пересечении  строки и  столбца ставится 1, в противном случае – 0.

Пример: ,  связаны отношением «меньше или равно»

Матрица отношения имеет вид

	1 2 3
1 2 3 4 5	1 1 1 0 1 1 0 0 1 0 0 0 0 0 0

Областью определения отношения  называют множество первых компонент кортежей , принадлежащих . Областью значений отношения  называют множество вторых компонент кортежей , принадлежащих .

Обратным отношением для отношения  называется множество

. Итак для получения достаточно поменять местами компоненты во всех парах, составляющих множество .

Пусть  - отношение на , а  - отношение на . Композицией отношений  и  называют новое отношение , определенное следующим образом:

.

Это множество обозначают .

Пример: , , . Отношение

Задано в виде , а отношение  задано множеством . Тогда композиция отношений  и  описывается множеством :   .

Свойства отношений

Рассмотрим свойства бинарных отношений, заданных на одном множестве:

Отношение  рефлексивно, если для всех  имеет место .

Примеры:  равно  на множестве натуральных чисел;

 делит  на множестве натуральных чисел.

Отношение  симметрично, если из  следует .

Пример: отношение «быть родственником»; отношение «быть симметричным относительно оси абсцисс».

Отношение   антисимметрично, если из   и  следует .

Пример: отношение «меньше или равно»: действительно, если  и , то .

Отношение  транзитивно, если из  и  следует  

Пример: отношение «учиться в одной группе».

Очень часто при решении  задач требуется проводить поиск элементов, обладающих заданным общим признаком. Оказывается, такие элементы связаны отношением эквивалентности.

Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Пример: отношение «одного возраста» на множестве людей;

«учится в одной группе» на множестве студентов НГТУ.

Важная задача, возникающая при научных исследованиях – это классификация объектов. При решении этой задачи нужен классификационный признак, по которому объекты относятся к тому или иному классу. Задача классификации решена, когда все множество объектов разбито на непересекающиеся подмножества, причем в каждом из подмножеств элементы эквивалентны.

Разбиением множества   называются непустые подмножества  множества , обладающие свойствами:

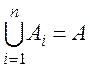 и  при .

Отношение «учится в одной группе» на множестве студентов НГТУ определяет разбиение множества студентов на множество групп.

Подмножество элементов, эквивалентных некоторому элементу  называется классом эквивалентности. В данном примере это группа.

Справедлива теорема: Если на непустом множестве  задано отношение эквивалентности, то оно разбивает  на различные классы эквивалентности.