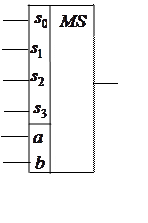
Приведем условные графические обозначения (УГО)
некоторых мультиплексоров:
 |
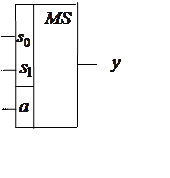2x1
4x1
Как выглядят УГО мультиплексоров 8x1 и 16x1?
Любую булеву функцию можно реализовать с помощью мультиплексора. Для этого аргументы функции подают на адресные входы мультиплексора, а значения функции на соответствующие селектируемые входы.
Пример. Реализовать на мультиплексоре функцию:
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Не следует думать, что число аргументов реализуемой функции должно быть обязательно равно числу адресных входов мультиплексора. Число аргументов может быть большим, но логика формирования селектируемых сигналов обычно усложняется.
Пример: Реализовать на мультиплексоре 4x1 функцию:
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
Подключим к адресным входам мультиплексора 4x1 два аргумента, например 
и 
. При таком подключении сигнал на адресном входе
совпадает с , а на входе 
с . Поскольку на первых четырех
наборах 
, то сигнал на
выходе мультиплексора совпадает с сигналом на шине 
. Нижняя строчка таблицы на наборах 0, 1, 2, 3
показывает какой сигнал должен формироваться на шине . Эти сигнал не постоянен, следовательно он
зависит от еще не учтенных аргументов 
и 
: 
. Легко увидеть, что логика формирования сигнала 
.
Рассуждая аналогично можно найти логику формирования
сигналов на остальных селектируемых шинах: 
, 
, 
.
 |
|||
 |
|
№ набора |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
Сигнал на Сигнал на Сигнал на Сигнал на
 |
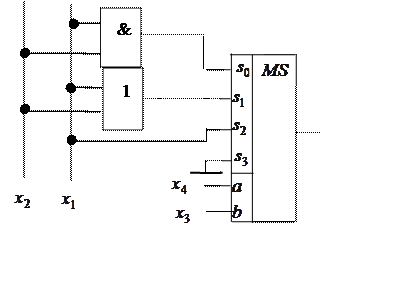Сложность логики, формирующей сигналы на селектируемых входах, зависит от того, какие аргументы подключены к адресным входам. Оптимальную схему можно получить, выполнив синтез для всех возможных комбинаций адресных сигналов.
Если брать мультиплексор с числом адресных входов на единицу меньше, чем число аргументов функции, то для реализации функции потребуется мультиплексор и, возможно, один инвертор.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
