Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 44

,

где

и спектральной плотностью

.

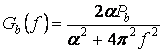Пусть поступающее на вход фильтра колебание

,                                                      (6.10)

где  задано уравнением (6.9),  – известная функция (несущее колебание), а  – гауссовский шум с нулевым средним и спектральной плотностью . Уравнение (6.9) называют уравнением состояния, а (6.10) – уравнением наблюдения. Исходя из условия оптимальной линейной фильтрации (6.7) и уравнений (6.9) и (6.10) , получают уравнения фильтра Калмана

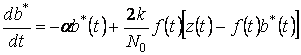,                                         (6.11)

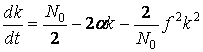.                                                             (6.12)

Уравнение (6.11) определяет структуру фильтра, а (6.12) – среднеквадратическую ошибку фильтрации . структурная схема фильтра Калмана для гауссовского сообщения при линейной модуляции приведена на рис. 6.3.

 

В качестве примера рассмотрим фильтрацию гауссовского марковского сообщения в канале с амплитудной модуляцией, когда для передачи сообщения  используется АМ сигнал с подавленной несущей. Тогда уравнение наблюдения

,

а уравнение оценки при периоде колебания Т много меньшем интервала корреляции   сообщения , т.е. при  или , уравнение оценки сводится к выражению

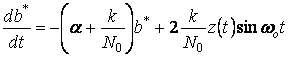.                                           (6.13)

Это уравнение моделируется линейным фильтром разомкнутого типа, приведенным на рис. 6.4. Постоянная времени , где , равная ошибке фильтрации определяется из уравнения  (6.12). Как видно, оптимальный фильтр для таких сигналов представляет схему синхронного детектора с интегрирующим  фильтром.

 В случае обычной амплитудной модуляции с несущей входной сигнал  и синхронный детектор выделяет огибающую , поэтому для получения на выходе оценки сообщения  в схе

му включены разделительный конденсатор , устраняющий постоянную составляющую , и аттенюатор А с коэффициентом затухания .

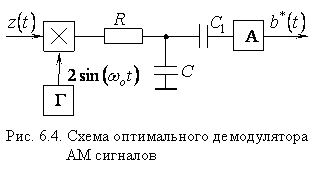В том случае, когда сигнал и шум стационарны, фильтр Калмана совершенно эквивалентен фильтру

Колмогорова-Винера. Однако для решения многих практических задач обработки сигналов фильтры Калмана по вычислительной структуре оказались более удобными, чем фильтры Колмогорова-Винера.

7. ЦИФРОВЫЕ МЕТОДЫ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ