Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 22

В этом случае исправляются 2 двойные, 8 тройных ошибок и 2 ошибки с кратностью 4.

Методом перебора получены два результата. В принципе метод может быть использован для получения нужного кода.

 Важной характеристикой  корректирующего кода является кодовое расстояние – наименьшее расстояние между кодовыми комбинациями, т.е. наименьшее число разрядов, в которых одна разрешенная кодовая комбинация отличается от другой. Если кодовое расстояние , то одиночная ошибка может превратить разрешенную комбинацию в другую разрешенную комбинацию. При этом одиночная ошибка остается необнаруженной. Очевидно, что для обнаружения одиночной ошибки нужно иметь , двойной –  и т.д.

Приведем (без доказательства) теорему об обнаруживающей способности кода: если код имеет   и используется декодирование по методу обнаружения ошибок, то все ошибки кратности обнаруживаются. Что же касается ошибок большей кратности, то одни из них обнаруживаются, а другие нет.

Существует аналогичная теорема об исправляющей способности кода: если код имеет   и используется декодирование с исправлением ошибок по наименьшему расстоянию, то все ошибки кратности исправляются. Что же касается ошибок большей кратности, то одни из них исправляются , а другие нет.

Для того, чтобы код мог обнаруживать все ошибки кратностью  и исправлять все ошибки кратностью , достаточно, чтобы кодовое расстояние удовлетворяло условию

.

При использовании канала со стиранием, часть разрядов принятого кода может быть стерта. Число таких разрядов назовем кратностью стирания . Такой код будет укороченным и иметь значимость  . Для того, чтобы такие комбинации кода могли быть отличимы друг от друга, расстояние между ними должно быть не меньше 1. Таким образом, для сохранения различимости кодовых комбинаций при стирании необходимо, чтобы  . Код с таким кодовым расстоянием восстанавливает стертые символы с кратностью , большей кратности исправляемых ошибок . Следовательно, восстанавливать стертые символы легче, чем исправлять ошибки.

Оценим вероятность ошибочного декодирования  (при декодировании с исправлением ошибок) и вероятность необнаруженной ошибки  ( при декодировании с обнаружением ошибок) в симметричном канале без памяти. В таком канале ошибка кратности  появляется с вероятностью

 .

Тогда

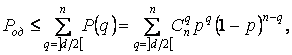
где - наименьшее целое большее или равное ;

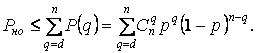
Очевидно, чем больше кодовое расстояние , тем меньше вероятности ошибочного декодирования и необнаруженной ошибки. Поэтому задача кодирования состоит в выборе кода, обладающего максимально возможным кодовым расстоянием. Решать ее можно увеличением разрядности кода  с сохранением числа разрешенных комбинаций  или уменьшением числа  с сохранением . Однако, такой путь нерационален. Обычно задачу поиска наилучшего кода ставят так: при заданных  и  найти код, имеющий наибольшее значение . В общем виде в теории кодирования эта задача не решена, хотя для многих значений   и  ее решения получены.