Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 42

Однополосная модуляция. Представляет собой перенос спектра сообщения вверх на частоту . При этом не меняются ширина спектра сигнала и соотношения между мощностями, поэтому .

Системы АМ, БМ и ОМ – линейные, поэтому приведенные выше соотношения для оптимального приемника справедливы как при слабых, так и при сильных помехах на входе. Эти соотношения определяют потенциальную помехоустойчивость.

Фазовая модуляция. Сигнал , где  – девиация фазы или индекс фазовой модуляции. Для такого сигнала ;  ; , а . При больших индексах модуляции , поэтому

;

.

Как видно, при ФМ выигрыш зависит от индекса модуляции и пик-фактора сообщения. Так как  может быть много больше единицы, то выигрыш в этой системе можно получить значительно больше единицы. Платой за выигрыш является расширение полосы частот, занимаемых сигналом. Приведенные соотношения справедливы для малого уровня шума на входе приемника.

Частотная модуляция. Сигнал . Энергетический спектр шума на выходе приемника ЧМ . При большом индексе модуляции , а полоса сигнала , выражения для выигрыша и обобщенного выигрыша

;

.

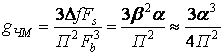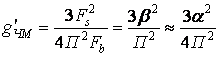При ЧМ так же, как и при ФМ, выигрыш может быть значительно больше единицы, и достигается за счет расширения полосы частот сигнала. Приведенные соотношения справедливы лишь при малом уровне помех.

Системы с ФМ и ЧМ имеют ярко выраженный пороговый эффект. Суть его состоит в том, что все широкополосные системы модуляции обеспечивают высокую помехоустойчивость при условии, что отношение сигнал/шум на входе приемника больше некоторого порогового значения. При отношении сигнал/шум меньше порогового широкополосные системы теряют свои преимущества (резко снижается помехоустойчивость) и связь становится невозможной.

6.3. Оптимальная линейная фильтрация непрерывных сигналов

Линейную фильтрацию широко используют в системах связи для обработки сигналов, так как они сравнительно легко синтезируются и просты в реализации. Кроме того, теория их построения развита, чего нельзя сказать о нелинейных фильтрах.

Линейные фильтры являются неотъемлемой частью любого приемного устройства. С их помощью осуществляется как додетекторная, так и последетекторная обработка сигналов. С их помощью сигналы разделяются в многоканальных системах связи. Требования к ним могут быть весьма различны в зависимости от назначения.

Пусть на вход линейного фильтра с импульсной характеристикой  поступает аддитивная смесь сигнала  и помехи

.

Требуется найти такую функцию , которая минимизирует средний квадрат ошибки

,

где  – оценка сигнала на выходе фильтра.