Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 32

Приведенные выше критерий требуют знания априорных вероятностей. На практике они часто неизвестны. В этом случае используют критерии максимального правдоподобия и Неймана-Пирсона.

Критерий максимального правдоподобия состоит в принятии решения о передаче сигнала , для которого отношение правдоподобия максимально:

.                                                                                          (5.4)

Очевидно, что и этот критерий является частным случаем критерия минимального среднего риска, когда все априорные вероятности и риски одинаковы.

Критерий Неймана-Пирсона используется при разработке радиолокационных приемников, когда априорные вероятности неизвестны, а последствия ошибок разного рода (ложной тревоги и пропуска цели) неодинаковы. Суть его состоит в том, что решающая схема считается оптимальной, если при заданной вероятности ложной тревоги  обеспечивается минимальная вероятность пропуска цели :

5.3. Принцип оптимальной фильтрации и синтез оптимальных сигналов

Пусть для передачи символа  используется сигнал . Предположим, что все искажения в канале строго детерминированы. В результате этого сигнал  преобразуется в сигнал . Случайной является только аддитивная помеха  в виде белого гауссовского шума со спектральной плотностью . Будем считать также, что все сигналы  имеют одинаковую длительность Т. Это имеет место в синхронных системах, при отсутствии в канале многолучевости и линейных искажений, либо при скорректированных искажениях. Синхронизацию системы будем считать точной, что позволяет принять момент начала посылки за нуль и наблюдать сигнал на интервале времени . Вопросы синхронизации являются весьма существенными при реализации оптимальных демодуляторов, но их рассмотрение выходит за рамки данного курса.

Таким образом, входной сигнал

.                                                             (5.5)

Для определения алгоритма работы оптимального (в смысле максимального правдоподобия) демодулятора необходимо найти отношение правдоподобия для всех  возможных сигналов относительно нулевой гипотезы (на вход поступает только аддитивная помеха) и выбрать из них максимальное.

Опуская эту громоздкую процедуру, приведем решающее правило

.

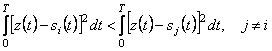В пространстве Гильберта 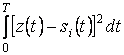 определяет квадрат расстояния между сигналами  и . Это позволяет придать решающему правилу простую геометрическую интерпретацию – оптимальный демодулятор регистрирует тот сигнал , который ближе к принятому колебанию. Схема, реализующая это правило содержит квадраторы, что затрудняет ее реализацию. Раскрыв скобки под знаком интеграла и сократив одинаковые слагаемые в обеих частях, получим

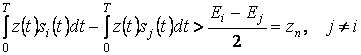,                               (5.6)

где - энергия сигнала .