Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 24

G=.

Здесь – двоичный символ (0 или 1), находящийся в -ом разряде -го кодового слова , входящего в выбранный базис.

Полученный таким образом код длины , содержащий 2^k комбинаций, обозначают (n,k). При заданных n и k существует много различных кодов. Они имеют различные порождающие матрицы и разные кодовые расстояния. Избыточность этих кодов , а скорость кода .

Если две порождающие матрицы отличаются только порядком расположения столбцов, то определяемые ими коды являются эквивалентными. Они имеют одинаковые кодовые расстояния и, следовательно, одинаковые способности обнаруживать и исправлять ошибки.

Чаще всего строят систематические линейные коды, в которых k символов являются информационными, а остальные n-k – проверочными. Примером простейшего систематического кода является код (n,n-1) с проверкой на четность. Такой код имеет  и позволяет обнаружить все нечетные ошибки.

После формирования всех разрешенных комбинаций  составляется множество комбинаций, ортогональных кодовым комбинациям. Ортогональная комбинация   должна удовлетворять условию

.

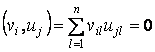Это должно быть выполнено для всех i и j.

Матрица Н, строками которой являются комбинации , называется проверочной. Она содержит n-k  строк и n столбцов. Строки этой матрицы линейно-независимы.

Обнаруживать и исправлять ошибки при систематическом коде можно следующим образом. Вычисляется исправляющая комбинация (синдром), составляющие которой представляют собой скалярные произведения принятой комбинации v_x и строк проверочной матрицы Н, т.е.

.

Комбинация c_j представляется (n-k) значным двоичным числом. Если ошибок нет, то синдром является нулевой комбинацией. Если имеется ошибка, то синдром – ненулевая комбинация, причем каждой комбинации соответствует свой вектор ошибки. Поэтому, определив синдром, мы будем знать вектор ошибки, а значит, иметь возможность исправить эту ошибку.

Применение такого кода позволяет при декодировании хранить (n-k) строк проверочной матрицы, а не список из 2^k комбинаций, и проверять выполнение (n-k)  равенств. Так при рассмотренном выше коде (100,50) следует хранить  символов вместо 10¹⁷ при табличном кодировании, и проверять 50 равенств вместо перебора 10¹⁵ расстояний.

В качестве примера рассмотрим построение кода (5,3) с минимальным кодовым расстоянием 2. Выберем образующую матрицу с линейно независимыми строками

G=.

Сформируем код, записав в качестве первой комбинации нулевую, следующих трех – строки образующей матрицы и остальных – линейные комбинации строк образующей матрицы. В результате получим код

v₁:     00000

v₂:00011

v₃:01101

v₄:11010

v₅:01110  v₂+ v₃

v₆:10111  v₃+ v₄