Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 37

В соответствии с моделью непрерывного канала со случайной начальной фазой сигнал на входе приемника

,

где  и  связаны преобразованием Гильберта;  – случайная начальная фаза сигнала.

Синтез алгоритма оптимального приема достаточно громоздок, поэтому, опуская его, приведем решающее правило:

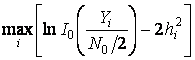,                                                              (5.20)

где ;  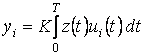 ;  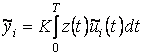 ;                (5.21)

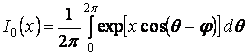 – модифицированная функция  Бесселя:

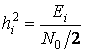 – отношение энергии сигнала к спектральной плотности белого шума на входе приемника.

Для двоичной системы сигналов правило оптимального некогерентного приема выражается неравенством:

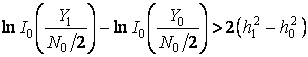.                                        (5.22)

Структурная схема оптимального некогерентного приемника приведена на рис 5.9.

 

Схема построена на базе квадратурных корреляционных каналов. Здесь Г₀ и Г₁ – соответственно генераторы опорных сигналов  и , 90^о – фазо-вращатель всех сигнальных составляющих на 90^о (преобразователь Гильберта). Величины  не зависят от начальной фазы сигнала и, как видно из (5.21), в момент времени Т  пропорциональны огибающей на выходе фильтра, согласованного с сигналом . Это говорит о том, что алгоритм приема можно реализовать на базе согласованных фильтров, как показано на рис. 5.10.

Идеальный детектор ДО выделяет огибающую напряжения на выходе согласованного фильтра.

Решающее правило существенно упрощается для систем, использующих сигналы с одинаковыми энергиями  (). Для них с учетом монотонного характера функции  алгоритм оптимального некогерентного приема записывается в виде

.

Для двоичной системы он сводится к проверке неравенства

.

При его выполнении регистрируется символ 1, в противном случае – 0. В этом случае алгоритм инвариантен относительно коэффициента передачи К и спектральной плотности шума . Именно это является основным преимуществом систем с активной паузой, определившим их широкое применение.

Исследование вероятности ошибок в канале с неопределенной начальной фазой и аддитивным гауссовским шумом при поэлементном приеме показало, что минимальную вероятность ошибки обеспечивает система с сигналами, удовлетворяющими условиям ортогональности в усиленном смысле

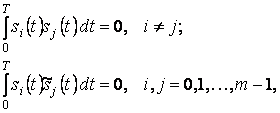                                              (5.23)

и равенства энергий

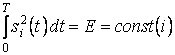.                                                                  (5.24)