Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 41

Для гармонического сигнала , а для телефонного сообщения .

Определим максимально возможные значения выигрыша и обобщенного выигрыша, когда непрерывное сообщение представляет собой гауссовский процесс с равномерным спектром в полосе частот  (квазибелый шум), а в канале существует аддитивная помеха в виде белого шума со спектральной плотностью .

Согласно теореме Шеннона передача сообщения с заданным значением  возможно в случае, когда эпсилон-производительность источника  меньше пропускной способности канала С. В рассматриваемом случае , а .

В гипотетической идеальной системе связи, использующей пропускную способность канала полностью, при  имеем . Тогда

.

Откуда при

.

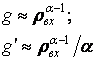В реальных системах пропускная способность используется лишь частично. Отношение эпсилон-производительности источника к пропускной способности канала , при которой обеспечивается заданная верность, т.е. , называют эффективностью системы связи. Для такой системы

.

Это означает, что при  можно обеспечить высокую верность (большое значение ) при относительно малых , т.е. получить большой выигрыш g.

Наилучшей считается система, обеспечивающая наибольшую помехоустойчивость при заданной эффективности, либо наибольшую эффективность при заданной помехоустойчивости.

В идеальной системе выигрыш  возрастает с увеличением  по показательному закону. Никакая реальная система не может обеспечить при заданном  более высокую помехоустойчивость, чем идеальная. Рассмотрим помехоустойчивость конкретных способов модуляции.

Амплитудная модуляция. Сигнал , где .

Энергетический спектр шума на выходе приемника АМ .

Мощность сигнала на входе приемника . При АМ , поэтому выигрыш и обобщенный выигрыши при оптимальном приеме

;

.

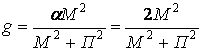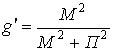Предельное значение выигрыша при АМ достигается при и  и равен 1. Практически всегда , а , поэтому  и .

Малые значения выигрыша обусловлены тем, что лишь небольшая часть мощности заключена в боковых полосах, несущих полезную информацию.

Балансная модуляция (модуляция с подавленной несущей). Сигнал . Средняя мощность сигнала . При  имеем , а . Следовательно, выигрыш при балансной модуляции не зависит от пик-фактора сообщения.