Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 30

Критерий оценки качества приема вероятностью правильного приема символа естественен, но не всегда возможен. Существуют и другие критерии качества.

Рассмотрим статистический подход к задаче приема дискретных сообщений на фоне шумов. Пусть при передаче дискретных сообщений используется код с основанием , а для передачи кодового символа  используется реализация . В течение тактового интервала времени  на вход приемного устройства поступает колебание , которое из-за искажений и помех в канале не совпадает в точности ни с одним из сигналов . Приемное устройство должно выбрать одну из  взаимоисключающих (альтернативных) гипотез: передавался сигнал  (символ ), передавался сигнал  (символ ), … .

Обратимся к геометрическому представлению сигналов, в соответствии с которым каждый сигнал отображается точкой (вектором) сигнального пространства как это показано на рис. 5.1.

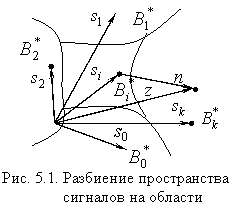Если помехи отсутствуют, то возможные значения колебания  изображаются векторами . При наличии помехи и передаче сигнала  вектор принимаемого колебания  отклоняется от вектора . Если пространство принимаемых сигналов разбить на  непересекающихся областей , каждая из которых соответствует определенной гипотезе, то получим некоторое решающее правило.

Различные приемные устройства отличаются друг от друга способом разбиения пространства сигналов на области . Обычно область содержит один вектор . В тех случаях, когда помеха не выводит вектор  за пределы области , решение оказывается верным. В противном случае возникает ошибка. Изменяя границы между областями, можно влиять на вероятность ошибочного приема отдельных передаваемых символов. Всегда существует такое расположение областей, которое в определенном смысле лучше всякого.

Если задан критерий качества, то наилучшее разбиение пространства принимаемых сигналов (оптимальная решающая схема) достигается методами теории статистических решений.

5.2. Критерии качества обнаружения и различения дискретных сигналов

Рассмотрим критерий идеального наблюдателя (критерий Котельникова), в соответствии с которым качество демодулятора оценивают безусловной вероятностью правильного приема символа.

Пусть имеется n-мерное евклидово пространство сигналов. В таком пространстве сигнал  характеризуется n-мерной плотность вероятности . Ее можно рассматривать как плотность вероятности коэффициентов разложения  по любому ортогональному базису. Если передается символ  (сигнал ), то можно определить условную n-мерную плотность вероятности , которую называют функцией правдоподобия i-ойгипотезы.