Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 12

– Если ансамбль содержит  различных сообщений, то . Равенство имеет место, если все сообщения равновероятны и независимы. Число  называют объемом алфавита источника. Для двоичного источника без памяти () энтропия максимальна при  и равна  бит.

Величина

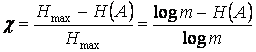
называется избыточностью источника с объемом алфавита . Она показывает, какая доля максимально возможной при этом алфавите энтропии не используется источником.

Как указывалось выше, энтропия ансамбля характеризует среднее количество информации, содержащейся в сообщении. Определим количество информации, содержащейся в одном ансамбле относительно другого, например, в принятом сигнале относительно переданного.

Пусть имеется объединение двух зависимых ансамблей A и B. Пусть – совместная вероятность реализаций  и . Совместная энтропия ансамблей  и

,

а условная энтропия

.

Поскольку , то

.

Для условной энтропии справедливо неравенство

,

причем , если, зная реализацию , можно точно установить реализацию  (в этом случае , а ), и , если знание реализации  не уменьшает неопределенности  (события  и независимые).

В общем случае условная энтропия  меньше безусловной  и знание реализации  снижает неопределенность реализации . Поэтому разность

называют количеством информации, содержащейся в  относительно , или взаимной информацией между  и .

.

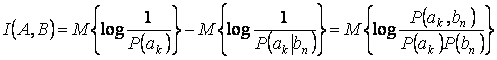Основные свойства взаимной энтропии:

– . Равенство имеет место, если  и  не зависимы.

– .

– . Равенство имеет место, если по реализации  можно однозначно восстановить .