Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 20

Идея возможности обнаружения ошибок крайне проста. Она состоит в том, что для передачи используют не все  возможных кодовых комбинаций, а лишь часть их . Используемые комбинации называют разрешенными, а остальные – запрещенными. Если в результате ошибок переданная комбинация превращается в одну из запрещенных, то обнаруживается ошибка. Если в результате ошибок переданная комбинация превращается в другую разрешенную, то ошибка не обнаруживается. Таким образом, из  возможных ситуаций ошибки будут обнаружены в  случаях. Доля обнаруживаемых ошибочных комбинаций

.

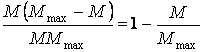Почти также просто дело обстоит и с исправлением ошибок. Для использования кода в качестве исправляющего множество запрещенных комбинаций  разбивается на  непересекающихся подмножеств , каждое из которых приписывается одной из разрешенных комбинаций . Способ приема состоит в следующем: если принята комбинация , то считается, что передана комбинация . Ошибка исправлена, если комбинация  действительно образовалась из . Ошибка всегда исправляется в  случаях при произвольном выборе подмножеств . Отношение числа исправленных ошибок к числу обнаруживаемых 

.

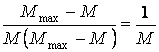Исправляющая способность кода зависит от способа приема, т.е. выбора разбиения .

Вектором ошибки  называют двоичную последовательность той же значности, что и кодовая комбинация, если на позициях, где произошла ошибка, стоят единицы, а на всех других – нули. Число единиц в векторе ошибки равно кратности ошибки. Принятая комбинация получается поразрядным сложением по  переданной комбинации и вектора ошибок. Векторы ошибок представляют все возможные сочетания ошибок и их число равно .

В качестве примера рассмотрим код с  и . Значит, число исправляемых комбинаций . Примем в качестве разрешенных комбинаций кода следующий набор:

.

Составим таблицу всех возможных комбинаций.

                                                                                                         Таблица 4.1.