Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 10

.

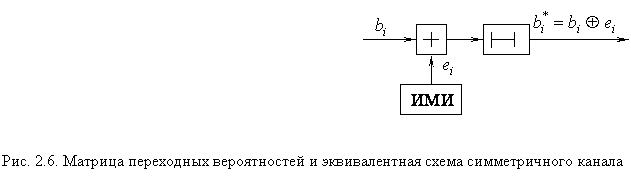
Двоичный симметричный канал полностью определяется статистикой последовательности мешающих импульсов , формируемой источником мешающих импульсов ИМИ и взаимодействующих с передаваемой последовательностью в сумматоре по модулю 2.

Двоичный канал является наиболее распространенным дискретным каналом. В этом случае . Например, символ  передается прямоугольным видеоимпульсом положительной полярности амплитудой , а  – видеоимпульсом отрицательной полярности.

Если непрерывный канал гауссовский, то сигнал на его выходе , а плотность вероятности помехи  с нулевым математическим ожиданием и дисперсией  –

.

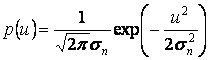При приеме сигнала методом однократного отсчета решающее правило следующее:

– В канале без стирания считается принятым символ b_i=1, если значение отсчета больше порогового , и символ , если значение отсчета меньше порогового.

– В канале со стиранием считается принятым символ b_i=1, если значение отсчета больше порогового ; символ , если значение отсчета меньше порогового , и произойдет стирание в остальных случаях.

Для канала без памяти  и стираний матрица переходных вероятностей

,

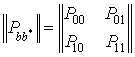где ;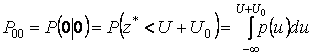

;

;

.

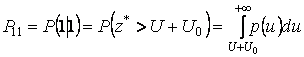Вероятность ошибочного приема символа

.

При  канал становится симметричным. В этом случае  и вероятность ошибки

,

где  – отношение сигнал/шум;

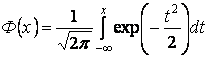 – интеграл вероятности.

Введение стирания позволяет уменьшить вероятность ошибки, но наряду с этим уменьшается вероятность правильного приема. Выбрав пороги такими, что , получим симметричный канал без ошибок.

В стационарном двоичном симметричном канале без памяти ошибки независимы, поэтому вероятность того, что в символах будет ошибок

.

Среднее число ошибок

.

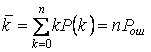Реальные каналы обычно сложнее, чем стационарный симметричный канал без памяти. Одним из важных отличий реальных каналов является наличие памяти, приводящей к группированию ошибок. Отрезок последовательности символов, в котором ошибки независимы и имеют высокую вероятность (близкую к ), называют пакетом ошибок. В остальной части последовательности вероятность ошибки близка к нулю.