По длине кодового слова коды делят на блочные и непрерывные. Блочными называют коды, в которых последовательности элементов сообщений источника разбиваются на отрезки и каждый из них преобразуется в определенную последовательность (блок) кодовых символов, называемых кодовой комбинацией. Непрерывные коды образуют последовательность кодовых символов, не разделяемую на последовательные кодовые комбинации, и в процессе кодирования символы определяются всей последовательностью элементов сообщения.
В
настоящее время чаще используются блочные коды, которые в свою очередь делят на
равномерные и неравномерные. В равномерных кодах все кодовые
комбинации содержат одинаковое число символов (разрядов), передаваемых по
каналу элементами сигнала неизменной длительности. Это позволяет упростить
технику передачи и приема сообщений, повысить помехоустойчивость синхронизации.
Число различных комбинаций ![]() разрядного
равномерного кода с основанием
разрядного
равномерного кода с основанием ![]()
![]() .
.
Если имеет место равенство, то код является простым или примитивным, т.к. для передачи используются все возможные комбинации.
Избыточность кода
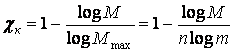 ,
,
а относительная скорость кода
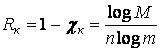 .
.
Если все
блоки равномерного кода передаются равновероятно и независимо друг от друга, то
![]() представляет собственную информацию
(энтропию), приходящуюся на каждый блок.
представляет собственную информацию
(энтропию), приходящуюся на каждый блок.
В
дальнейшем будем рассматривать двоичные (бинарные) коды, имеющие
основание 2. Множество всех возможных двоичных блоков или кодовых векторов
длины ![]() образует линейное пространство,
если:
образует линейное пространство,
если:
– операция сложения осуществляется как поразрядное
сложение по ![]() . Например,
. Например, ![]() ;
;
– норма вектора определяется как число единиц в блоке
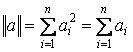 ;
;
– расстояние между векторами – число разрядов, в которых символы не совпадают,
 .
.
Скалярное произведение в этом пространстве
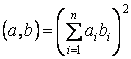 .
.
4.2. Неравномерные эффективные коды
Неравномерные блочные коды используют практически только для кодирования источников с целью уменьшения или устранения избыточности. Идея такого кодирования состоит в том, что более вероятные сообщения кодируются короткими блоками, а менее вероятные – длинными. В результате средняя длина блока уменьшается. При этом важно обеспечить однозначность декодирования.
Например, алфавит источника содержит шесть сообщений А,Б,В,Г,Д,Е, передаваемых с вероятностями 0,4; 0,3; 0,1; 0,08; 0,07; 0,05 соответственно. Сумма вероятностей равна 1. Энтропия источника
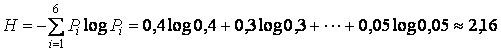 .
.
При кодировании сообщений равномерным двоичным блочным кодом на каждое сообщение необходимо затратить 3 символа. В соответствии с теоремой кодирования эти сообщения можно закодировать так, что среднее число символов в сообщении будет равно 2,16+e.
Допустим
кодирование произведено следующим образом: А – 0 Б – 1 В – 00 Г –
01 Д – 10 Е –11. Наиболее вероятные сообщения А и Б закодированы одним
символом, а остальные – двумя. В этом случае среднее число символов на
сообщение ![]() , т.е. меньше, чем по теореме
кодирования. Это объясняется тем, что выбранный код не обеспечивает
однозначного декодирования. Так последовательность 00110100011110 декодируется
как ААББАБАААББББА, или ВЕГВГЕД, или ААЕГАВБЕД и так далее. Можно после каждого
элемента кода ставить пробел (как в коде Морзе), но это будет уже троичный код
и
, т.е. меньше, чем по теореме
кодирования. Это объясняется тем, что выбранный код не обеспечивает
однозначного декодирования. Так последовательность 00110100011110 декодируется
как ААББАБАААББББА, или ВЕГВГЕД, или ААЕГАВБЕД и так далее. Можно после каждого
элемента кода ставить пробел (как в коде Морзе), но это будет уже троичный код
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.