Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 11

3. Основы теории информации

3.1. Информационные параметры сообщений и сигналов

Для сравнения различных источников сообщений и каналов связи необходима мера информации, содержащейся в сообщении и переносимой сигналом. Строгие методы количественного определения информации предложены К. Шенноном в 1948 г. Они легли в основу теории информации, являющейся математической основой теории связи.

Рассмотрим основные идеи этой теории применительно к дискретному источнику. Пусть источник посылает сообщение  из некоторого ансамбля , т.е. . Количество информации, содержащейся в этом сообщении, должно удовлетворять естественным требованиям:

– количество информации должно быть аддитивной величиной, т.е. в двух независимых сообщениях оно должно равняться сумме количества информации в каждом из сообщений;

– количество информации в сообщении о достоверном событии равно нулю;

– количество информации не должно зависеть от качественного содержания сообщения.

Из этих требований следует, что определение количества информации должно основываться на параметре, характеризующем сообщение в общем виде, например, вероятности  того, что источник посылает данное сообщение. Но вероятность появления двух независимых событий

,

а количество информации должно быть аддитивной величиной. Очевидно, что

, если .

Для достоверного события , откуда , что удовлетворяет второму требованию. Поскольку , то для получения неотрицательного значения количества информации примем . Итак,

.

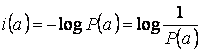Обычно основание логарифма берут равным 2. Единица информации при этом носит название двоичная единица или бит. 1 бит равен количеству информации в сообщении о событии, происходящем с вероятностью 0,5. Количество информации в сообщении тем больше, чем оно менее вероятно, или иначе, чем оно более неожиданно.

Приведенное количество информации является случайной величиной, поскольку сами сообщения случайные. Его распределение вероятностей зависит от распределения вероятностей сообщений  в данном ансамбле. Для характеристики всего ансамбля (источника) сообщений используется математическое ожидание количества информации, называемое энтропией

.

Чем больше энтропия источника, тем больше степень неожиданности передаваемых им сообщений в среднем и тем более неопределенным является ожидаемое сообщение. Поэтому энтропию называют мерой неопределенности сообщений. Неопределенность существует до передачи. После правильного приема она устраняется, поэтому количество информации можно трактовать как меру уменьшения неопределенности.

Энтропия является основной характеристикой источника. Чем она выше, тем труднее запомнить сообщение и передать его по каналу связи. Как правило, затраты энергии, необходимой для передачи сообщения, пропорциональны его энтропии.

Основные свойства энтропии.

– Энтропия неотрицательна. Она равна нулю только для вырожденного ансамбля, когда одно сообщение передается с вероятностью 1, а остальные – 0.

– Энтропия аддитивна – если рассматривать  последовательно передаваемых сообщений как одно крупное сообщение, то энтропия такого укрупненного сообщения равна сумме энтропий составляющих.