Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 43

Для случая, когда  и  – стационарные взаимно-некоррелированные процессы с известными энергетическими спектрами  и , задача была решена независимо друг от друга А.Н. Колмогоровым и Н. Винером, поэтому оптимальный (в указанном смысле) линейный фильтр называют фильтром Колмогорова _Винера. Фильтр физически реализуем, если его импульсная характеристика равна нулю при отрицательных значениях аргумента. Фильтр будет оптимальным, если ошибка некоррелирована с входным сигналом для всех значений :

.                                                                          (6.7)

Для реализуемого фильтра , а для нереализуемого .

Фильтр будет оптимальным, если его импульсная характеристика удовлетворяет уравнению Винера-Хопфа

.

Уравнение легко решается для нереализуемых фильтров, когда . Применив преобразование Фурье к обеим частям, получим

.

Отсюда частотный коэффициент передачи оптимального линейного фильтра

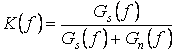
или в более общем случае, когда учитывается задержка в фильтре,

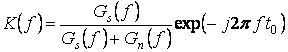.                                              (6.8)

Ошибка при этом

.

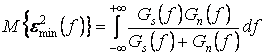Ошибка равна нулю только в том случае, когда , т.е. спектры сигнала и помехи не перекрываются. Во всех остальных случаях оптимальный фильтр пропускает различные частоты с тем меньшим весом, чем больше отношение  при данной частоте. Увеличивая время запаздывания, можно приблизиться к (6.7) и в случае реализуемого фильтра.

Если требуется реализовать фильтр без существенного запаздывания, то задача существенно усложняется. В этом случае используют выражение для частотного коэффициента передачи (6.7) и раскладывают его на несколько составляющих, выделяя оптимальную реализуемую часть. В общем случае оптимальным по критерию минимума среднеквадратической ошибки является нелинейный фильтр. Исключение представляет случай, когда сигнал и помеха являются гауссовскими. для них оптимальный фильтр всегда линеен.

Фильтр Колмогорова-Винера является оптимальным для выделения (оценки) стационарного сигнала. Модулированные сигналы имеют конечную длительность и не являются стационарными.

Существует  другой подход к синтезу оптимального фильтра: определяют не сами характеристики оптимального фильтра, а дифференциальные уравнения, моделирующие этот фильтр. В теории линейной фильтрации такой подход был применен Калманом и Бьюси. Условие стационарности сигнала и помехи при этом не является обязательным. Дополнительно предполагается, что фильтруемое сообщение  порождается линейным стохастическим дифференциальным уравнением

.                                                                          (6.9)

Физически это означает, что сообщение  рассматривают как результат прохождения стационарного белого шума  через линейную цепь, в данном случае через интегрирующую RC цепочку с постоянной . Сформированное таким образом сообщение является гаусссовским марковским процессом с функцией корреляции