Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 14

,

где  и  – случайные процессы на входе и выходе канала.

Из четырех энтропий в этом выражении только  не зависит от свойств канала и определяет собственную информацию источника сообщений. Допустим, что на вход канала можно подавать символы от разных источников ( и  одинаковые,  разные). Для каждого источника количество информации, переданной по каналу, будет разное. Максимальное количество переданной информации, взятое по всем возможными источникам входного сигнала, характеризует сам канал и называется пропускной способностью канала в расчете на один символ

 бит/символ.

При расчете пропускной способности канала в расчете на единицу времени

 бит/с.

Определим пропускную способность симметричного канала без памяти.

;

,

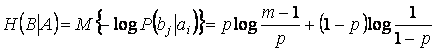так как, если , то  с вероятностью ();

если , то  с вероятностью .

Очевидно, что для определения пропускной способности необходимо максимизировать значение . Оно будет максимальным при равновероятной передаче символов и равным . Поэтому пропускная способность

.

Для двоичного симметричного канала () будем иметь

.

Зависимость пропускной способности двоичного симметричного канала от вероятности ошибочного приема символа  приведена на рис. 3.1.

При  пропускная способность двоичного канала равна нулю, так как при такой вероятности ошибки последовательность выходных символов можно получить, не передавая сигналы по каналу, а выбирая их наугад. В этом случае последовательности на входе и выходе канала независимы. Случай, когда , называют обрывом канала.

При  пропускная способность канала такая же, как и при  (канал без помех). Объясняется это тем, что при  для получения правильного сигнала достаточно инвертировать все выходные символы.

3.4. Пропускная способность непрерывного канала

Пусть канал имеет полосу пропускания шириной . Тогда сигналы на его входе  и выходе  в соответствии с теоремой Котельникова определяются своими отсчетами, взятыми через интервал , а количество информации, переданной за время , равно сумме количества информации, переданной каждым отсчетом.

Пропускная способность канала на один отсчет