Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 23

Эффективность помехоустойчивого кода возрастает при увеличении его длины, т.к. в этом случае уменьшается вероятность ошибочного декодирования.

На первый взгляд помехоустойчивое кодирование реализуется достаточно просто. В память кодера записываются разрешенные комбинации выбранного кода и правило сопоставления одному из  сообщений одной из комбинаций кода. Это правило известно в декодере. Там принятая комбинация сравнивается со всеми комбинациями списка и отыскивается та, которая ближе к принятой. Однако даже при небольших  такой способ весьма сложен.

В качестве примера рассмотрим код при скорости кода . Тогда из  следует, что . Таким образом, кодовая таблица должна содержать 10¹⁵ кодовых комбинаций или  кодовых символов. Изготовление такого запоминающего устройства в настоящее время нереально. С другой стороны, при декодировании необходимо выполнить  операций сравнения. При работе в реальном времени это необходимо сделать за время, не превосходящее длительность комбинации. Пусть длительность комбинации равна 1 с, тогда даже при скорости

10⁹  операций в секунду необходимо иметь 10⁸ параллельно работающих схем!

Таким образом, применение достаточно эффективных (значит, и достаточно длинных) кодов при табличном методе кодирования и декодирования технически невозможно. Поэтому основные направления теории помехоустойчивого кодирования заключаются в поисках таких классов кодов, для которых кодирование и декодирование ведется не перебором таблиц, а с помощью некоторых регулярных правил. Один из таких классов представляют линейные коды, которые в свою очередь содержат подклассы, отличающиеся теми или иными свойствами. Некоторые из них позволяют упростить построение кодера и декодера даже при . Оказывается выгодным применять коды с кодовым расстоянием меньше оптимального, если их структура позволяет упростить кодек.

4.4. Линейные двоичные блочные коды

Линейными называют такие двоичные коды, в которых множество всех разрешенных комбинаций является линейным пространством относительно операции поразрядного сложения по модулю два. Очевидно, что это пространство является подпространством линейного пространства, образуемого множеством всех комбинаций длины . Чтобы разрешенные комбинации были линейным пространством, они должны содержать нулевой элемент (комбинацию, состоящую из одних нулей), а поразрядная сумма по  любых разрешенных блоков должна быть также разрешенным блоком. Линейные коды иногда называют групповыми.

Двоичный линейный код можно построить следующим образом. Среди 2ⁿ комбинаций различными способами можно найти n линейно-независимых (например, ортогональных). Выберем из них k линейно-независимых комбинаций  и образуем все возможные линейные комбинации

,

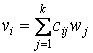где – весовой коэффициент, принимающий значения 0 или 1, суммирование является поразрядным по .

Множество  образует линейное пространство, содержащее 2^k комбинаций, т.е. линейный код. Обычно выбранные линейно-независимые комбинации записывают в виде матрицы размером , которую называют производящей или порождающей матрицей кода . В общем случае она имеет вид