Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 13

– . Свойство аналогично предыдущему.

– . Это позволяет интерпретировать энтропию как собственную информацию.

Итак,

– энтропия ансамбля  представляет собой максимальное количество информации, которое может содержаться в  относительно любого другого ансамбля ;

– для того, чтобы восстановить реализацию ансамбля  в точности, необходимо передать в среднем количество информации, равное его энтропии.

3.2. Информация в непрерывных сигналах

Обобщим понятие энтропии и взаимной информации на ансамбли непрерывных сигналов. Пусть s – непрерывная случайная величина с плотностью вероятности . Разобьем область значений s на небольшие интервалы длительностью . Вероятность того, что  равна . Энтропия дискретного ансамбля равна . Если устремить  к нулю, то в пределе должна получиться энтропия непрерывного сигнала

.

Второе слагаемое стремится к бесконечности и не зависит от распределения вероятности сигнала. Это означает, что энтропия (собственная информация) любой непрерывной случайной величины бесконечно велика.

Первое слагаемое является конечным и полностью определяется плотностью вероятности. Его называют дифференциальной энтропией и обозначают :

.

Дифференциальная энтропия в отличие от обычной энтропии не является мерой собственной информации. Информационный смысл имеет разность дифференциальных энтропий.

Определим взаимную информацию между двумя непрерывными случайными величинами  и , проводя рассуждения аналогичные предыдущим,

.

Таким образом, взаимная информация между непрерывными величинами и  равна разности дифференциальной энтропии  и условной дифференциальной энтропии . Как видно, форма выражения для взаимной информации между непрерывными величинами совпадает с формой аналогичного выражения для дискретных величин.

Найдем дифференциальную энтропию гауссовской случайной величины с математическим ожиданием  и дисперсией . По определению

.

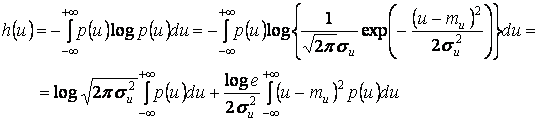Первый интеграл по условию нормировки равен 1, второй по определению – дисперсии . Поэтому

.

Таким образом, энтропия гауссовской случайной величины не зависит от математического ожидания и монотонно возрастает с увеличением дисперсии.

Особо следует отметить, что из всех непрерывных случайных величин с одинаковой дисперсией наибольшую дифференциальную энтропию имеет величина с нормальным распределением.

3.3. Пропускная способность дискретного канала связи

Рассмотрим дискретный канал, через который в единицу времени передается  символов из алфавита объемом . При передаче каждого символа в среднем по каналу проходит количества информации