Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 15

  бит/отсчет,

а пропускная способность в расчете на единицу времени

 бит/с.

Определим пропускную способность непрерывного канала без памяти с аддитивным белым гауссовским шумом и полосой пропускания , если мощность сигнала не превышает , а мощность шума в пределах полосы пропускания .

Итак, . Условная плотность вероятности  имеет нормальное распределение, поэтому в соответствии с п. 3.2 дифференциальная энтропия . Найдем плотность вероятности , при которой максимизируется . Учитывая, что  и  независимые случайные величины, то дисперсия

является постоянной величиной. А при постоянной дисперсии максимальную энтропию имеет нормально распределенная случайная величина, т.е.

.

Откуда

.

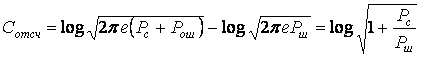Информация, переданная несколькими отсчетами максимальна, если отсчеты независимы. Отсчеты, взятые в соответствии с теоремой Котельникова, некоррелированы, а поскольку они гауссовские, то и независимы. Отсюда

.

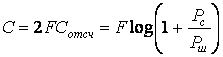Это известная формула Шеннона, имеющая важное значение в теории связи, так как определяет зависимость пропускной способности канала связи от полосы пропускания и отношения сигнал/шум. Она указывает на возможность обмена мощности сигнала на полосу пропускания.

Для выяснения зависимости  пропускной способности от частоты заменим :

.

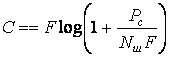Это возрастающая функция стремится к  при . Используя  это выражения можно показать, что для передачи одного бита информации необходима энергия сигнала .

4. Основы теории кодирования

4.1. Назначение и классификация кодов

В широком смысле кодированием называют любое преобразование сообщения в сигнал путем установления взаимного соответствия. Однако обычно этот термин используют в узком смысле, когда рассматривают кодирование сообщений в дискретном канале. Дискретный канал образуется из непрерывного путем включения в канал модема. На вход модулятора и с выхода демодулятора поступают дискретные кодовые символы, одинаковые или различные. Будем обозначать кодовые символы числами , где  – основание кода.

Пусть источник выдает некоторое дискретное сообщение , которое можно рассматривать как последовательность элементов сообщения или знаков . Совокупность всех возможных элементов сообщения называют алфавитом источника. Кодирование заключается в том, что последовательность элементов сообщения  заменяется кодовым словом  (последовательностью кодовых символов). Такое преобразование, как правило, взаимно-однозначное, что позволяет осуществить декодирование, т.е. восстановление сообщения по кодовому слову.