Изучение методов решения разнообразных задач, возникающих при передаче информации от ее источника к получателю, страница 31

Пусть, на вход демодулятора в течение интервала  приходит элемент колебания , и демодулятор принимает решение о передаче символа . Вероятность принятия правильного решения равна вероятности  передачи символа  при  условии прихода реализации элемента сигнала . Эту вероятность называют апостериорной вероятностью символа .

Вероятность правильного приема будет максимальной, если решающая схема относит реализацию элемента приходящего сигнала  к той области , для которой апостериорная вероятность  максимальна. Таким образом, критерий идеального наблюдателя обеспечивается решающей схемой, построенной по правилу максимума апостериорной вероятности. Решение  принимается в том случае, когда выполняется система неравенств

.                        (5.1)

или    .

Для двоичной системы при выполнении неравенства   регистрируется символ 1, в противном случае – 0.

Используя формулу Байеса

,

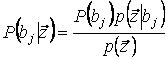где  – априорная вероятность передачи символа , решающее правило (5.1) можно привести к виду

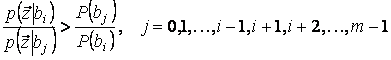.                         (5.2)

Отношение в левой части называют отношением правдоподобия двух гипотез – о том, что передавался символ , и о том, что передавался символ . Это отношение обычно обозначают . Если все символов равновероятны, то есть , правило упрощается

.

Критерий идеального наблюдателя является не единственным критерием оптимальности решающей схемы. В случаях, когда различные ошибки приводят к различным последствиям, например, в системе автоматической пожарной сигнализации, используют критерий минимума среднего риска. В этом случае каждой ситуации  ставится в соответствие некоторая плата (риск) . Правильному приему дается нулевой риск. Чем более нежелательна ситуация, тем больше значение риска. Усредняя риски по всем возможным значениям и  с учетом вероятностей, получим средний риск

.

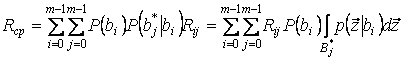Критерий минимального среднего риска заключается в том, что оптимальной считается решающая схема, обеспечивающая . Приемник, работающий по такому правилу, называется байесовским. В таком приемнике чаще возникают ошибки, связанные с малым риском, и реже – с большим.

Решающее правило в этом случае можно привести к виду

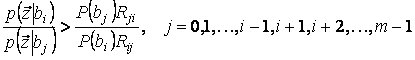.                    (5.3)

Очевидно, что критерий идеального наблюдателя является частным случаем критерия минимального среднего риска, когда все риски одинаковы.