 |
5.5. Помехоустойчивость оптимального приема детерминированных
сигналов
Определим потенциальную помехоустойчивость двоичной
системы с аддитивным белым шумом, когда при приеме точно известны оба ожидаемых
сигнала ![]() и
и ![]() ,
полагая, что априорные вероятности сигналов одинаковы.
,
полагая, что априорные вероятности сигналов одинаковы.
Алгоритм оптимального приема в этом случае имеет вид:
 .
.
При выполнении неравенства
реализуется символ 1, в противном случае – 0. Допустим, передавался символ 1 (сигнал
![]() ). Тогда вероятность ошибки
). Тогда вероятность ошибки ![]() определится вероятностью выполнения
неравенства
определится вероятностью выполнения
неравенства
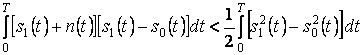 ,
,
которое легко сводится к неравенству
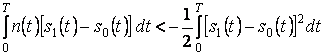 . (5.12)
. (5.12)
Аналогичное выражение
получается и при передаче символа 0, т.е. ![]() ,
а дискретный канал является симметричным. Последнее выражение перепишем в виде
,
а дискретный канал является симметричным. Последнее выражение перепишем в виде
![]() , (5.13)
, (5.13)
где
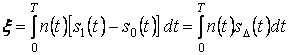 – случайная составляющая сигнала на
входе решающего устройства;
– случайная составляющая сигнала на
входе решающего устройства;
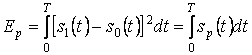 – энергия разностного сигнала.
– энергия разностного сигнала.
Если ![]() – гауссовский
стационарный белый шум с нулевым средним и двусторонней спектральной плотностью
мощности
– гауссовский
стационарный белый шум с нулевым средним и двусторонней спектральной плотностью
мощности ![]() , то
, то ![]() также
распределена по гауссовскому закону, т.к. формируется из
также
распределена по гауссовскому закону, т.к. формируется из ![]() линейным преобразованием. Найдем
математическое ожидание и дисперсию случайной величины
линейным преобразованием. Найдем
математическое ожидание и дисперсию случайной величины ![]() :
:
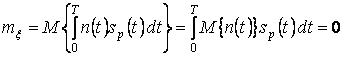 ;
;
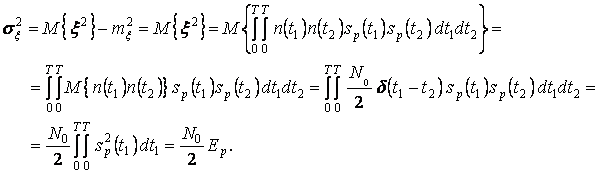
Так как ![]() распределена по
гауссовскому закону, то вероятности ошибки, равная вероятности выполнения неравенства
(5.13),
распределена по
гауссовскому закону, то вероятности ошибки, равная вероятности выполнения неравенства
(5.13),
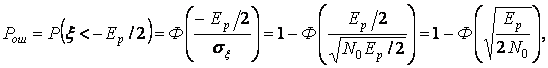
![]() (5.14)
(5.14)
где 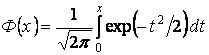 –
табулированный интеграл вероятности.
–
табулированный интеграл вероятности.
Как видно из (5.14), помехоустойчивость определяется
разностной энергией ![]() , равной квадрату
расстояния между сигналами в пространстве Гильберта, и спектральной плотностью
белого шума. Помехоустойчивость не зависит от формы сигнала.
, равной квадрату
расстояния между сигналами в пространстве Гильберта, и спектральной плотностью
белого шума. Помехоустойчивость не зависит от формы сигнала.
На рис 5.7 приведено геометрическое представление сигналов двоичной системы.
 |
Из рисунка видно, что в системе с АМ ![]() , и тогда
, и тогда
 , где
, где 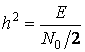 ; (5.15)
; (5.15)
в системе с ЧМ ![]() и
и
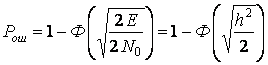 ; (5.16)
; (5.16)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.