Логопериодические вибраторные антенны: Учебное пособие, страница 69

.                     {7.1}

Далее необходимо определить массив проводимостей шлейфов. Отметим, что при составлении программ расчёта оказывается удобным выбрать матрицу шлейфов [Yh] размером 2N-1, хотя общее количество шлейфов – N-1. При этом собственно проводимости шлейфов имеют только нечётные номера – 1, 3, 5 и так далее. Электрическая длина шлейфа выбирается в зависимости от длины соседнего (более длинного) вибратора как произведение длины вибратора на коэффициент ks (ks < 1). Проводимость разомкнутого на конце шлейфа определяется обычным образом

,                                          (7.1)

где Wh – волновое сопротивление линии шлейфа, kh – коэффициент фазы линии шлейфа, lh – длина шлейфа.

Длина шлейфа может быть укорочена путём подключения сосредоточенной ёмкости на конце шлейфа. Проводимость укороченного шлейфа с сосредоточенной ёмкостью можно определить из следующего соотношения

,                          (7.2)

где C – величина сосредоточенной ёмкости.

Применение укорачивающих ёмкостей только усложняет конструкцию антенны и не даёт особых преимуществ. Поэтому укорачивающие ёмкости в дальнейшем не рассматриваются.

Учёт тепловых потерь в линиях шлейфов производится аналогично учёту этих потерь в распределительном фидере, как это было рассмотрено в 3 главе.

Построим функцию для расчёта проводимостей шлейфов. Предварительно необходимо рассчитать массив длин шлейфов. Принято длину шлейфа определять через длину соседнего вибратора:

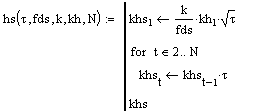,                              {7.2}

где fds – коэффициент замедления фазы волны в линии шлейфа, k – отношение длины шлейфа к длине соседнего вибратора, kh₁ – длина первого вибратора. Функция для расчёта проводимостей шлейфов:

,               {7.3}

где tes – составляющая тепловых потерь в линии шлейфа, ws – волновое сопротивление линии шлейфа.

Зная матрицы проводимостей фидера [Y1] и проводимостей шлейфов [Yh], можно получить обычную матрицу проводимостей фидера [Y] с учётом шлейфов методами теории цепей [15]. Собственная проводимость в точке подключения первого вибратора:

.                                     (7.3)

Собственная проводимость в точке подключения N-го вибратора:

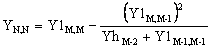,                                (7.4)

где M=2N-1.

Собственная проводимость в точке подключения n-го вибратора:

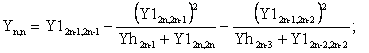
.                                                               (7.5)

Взаимная проводимость между точками подключения n-го и n-1-го вибраторов:

.                           (7.6)

Функция для расчёта матрицы проводимостей фидера [Y]:

{7.4}

где f и t – коэффициент замедления фазы и составляющая тепловых потерь в фидере соответственно, yy0(f,t,dl,kh,kll,w,M) – функция {3.6}.

Предлагается использовать шлейфы и фидер в микрополосковом исполнении, однако, можно анализировать эту антенну и в классическом варианте. Для классического варианта волновое сопротивление  линии, состоящей из цилиндрического проводника радиуса r и его зеркального отображения, расположенного на расстоянии D определяется выражением (1.14). В этом случае расстояние от центра проводника до металлической поверхности равно . Функцию для определения Dl получаем из {2.6} уменьшив D в два раза: