Функция для расчёта ДН одиночного вибратора (1.44)
 , {2.14}
, {2.14}
а полная функция для расчёта ДН ЛПВА (1.43)
 .{2.15}
.{2.15}
В функциях для расчёта ДН аргумент I – вектор-столбец токов в вибраторах [I], остальные аргументы понятны по наименованию.
Функцию для входного сопротивление ЛПВА вычисляем согласно (1.46)
 , {2.16}
, {2.16}
где Z – матрица ![]() ; I –
вектор-столбец токов в вибраторах; N – количество вибраторов.
; I –
вектор-столбец токов в вибраторах; N – количество вибраторов.
Расчёт
КСВ производится обычным образом – по заданному входному сопротивлению ![]() и реальному входному сопротивлению
и реальному входному сопротивлению ![]() .
.
 , {2.17}
, {2.17}
где rwx – заданное входное сопротивление; zin – реальное входное сопротивление. В первом операторе функции {2.17} вычисляется комплексный коэффициент отражения, во втором – КСВ.
Для
расчёта КНД, согласно (1.42), необходимо определить модуль максимума ДН и
действительную часть входного сопротивления. Модуль максимума ДН необходим и
для нормирования при выводе графиков. При выбранной нами системе координат
(рис. 1.1) максимум ДН приходится на углы ![]() ,
, ![]() . В результате
. В результате
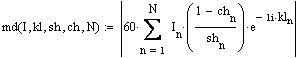 . {2.18}
. {2.18}
Функцию для расчёта КНД получаем из (1.42)
![]() , {2.19}
, {2.19}
где md – модуль максимума ДН; zin – входное сопротивление ЛПВА.
Для трёхчленного закона распределения тока элементы матрицы системы линейных алгебраических уравнений и правой части описываются выражением (1.37б). Составлять программы начнём с подынтегральных выражений. Этих выражений согласно (1.41), как и интегралов, три, поскольку ток описывается тремя гармониками. Выражения состоят из произведения двух функций – гармоник распределения тока (1.41) и ядра (1.31). Функция для расчёта ядра {2.11} уже была рассмотрена ранее. Для гармоник распределения тока получаем
![]() , {2.20}
, {2.20}
![]() , {2.21}
, {2.21}
![]() . {2.22}
. {2.22}
Аргументы этих функций, за исключением
массива ![]() , описывались. Массив чисел
, описывались. Массив чисел ![]() следует вычислить заранее, чтобы во
время интегрирования не загружать процессор компьютера бессмысленной работой.
Также нужен и массив чисел
следует вычислить заранее, чтобы во
время интегрирования не загружать процессор компьютера бессмысленной работой.
Также нужен и массив чисел ![]() , который будет
необходим при расчёте ДН
, который будет
необходим при расчёте ДН
 , {2.23}
, {2.23}
 . {2.24}
. {2.24}
В аргументах выражений (1.37а) и
(1.37б) имеются числа ![]() . Введём функцию
для расчёта этих чисел
. Введём функцию
для расчёта этих чисел
 . {2.25}
. {2.25}
Во втором члене ядра (1.31) в
соответствии с (1.37б) имеется множитель ![]() ,
а в (1.37а) и (1.37б) – множитель
,
а в (1.37а) и (1.37б) – множитель ![]() . Они
рассчитываются функциями {2.8} и {2.9}, соответственно, с заменой аргумента kh на kh3, а аргумента N – на
3N.
. Они
рассчитываются функциями {2.8} и {2.9}, соответственно, с заменой аргумента kh на kh3, а аргумента N – на
3N.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.