Логопериодические вибраторные антенны: Учебное пособие, страница 24

Однако, «оптимальное» значение  может привести к слишком большой длине антенны и в этом случае понятие «оптимальности»  находится под вопросом, так как вполне может оказаться, что более короткая антенна с большим числом вибраторов гораздо экономичнее длинной антенны с «оптимальным» .

При проектировании антенны приведенные на рис. 2.1 графики можно использовать для выбора начального приближения. Хотя эти данные носят приближенный характер, так как рассчитывались для антенн с высоким входным сопротивлением ( Ом) и конкретным отношением длины вибратора к радиусу (), они позволяют качественно оценить ожидаемый результат. А «оптимальные» параметры можно получить после расчёта и сравнения нескольких вариантов, тем более что критерий оптимальности в каждом конкретном случае может быть свой.

Далее, необходимо найти число элементов (вибраторов) антенны. Это число определяется коэффициентом перекрытия рабочего диапазона частот  (где  и  – максимальная и минимальная частоты рабочего диапазона соответственно) и шириной активной области . Ширина активной области  определяет количество вибраторов, попадающих в активную область. Общий коэффициент перекрытия (отношение длины первого вибратора к длине последнего вибратора) получается как . Для определения ширины активной области можно использовать номограмму [5], где приведены зависимости  от угла  для различных  при  Ом и.

Более простой метод определения необходимого числа вибраторов предложен в [21]. На основе результатов численного анализа предлагается выбирать следующие длины самого короткого и самого длинного вибраторов

; ,                               (2.2)

где ,– минимальная и максимальная длина волны рабочего диапазона частот ЛПВА, соответственно.

Учитывая, что размеры вибраторов связаны законом геометрической прогрессии

получим из (2.1) коэффициент перекрытия по частоте

                      (2.3)

и необходимое число вибраторов

.         (2.4)

Будем предполагать, что читатели знакомы с языком программирования Mathcad, поэтому основы программирования ниже не описываем. Для разрабатываемых функций (программ) введём цифровое обозначение, подобное обозначению формул, но в фигурных скобках. Выражение (2.4) запишем в виде функции на языке программирования Mathcad для расчёта необходимого числа вибраторов

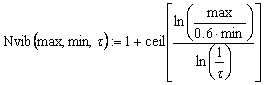,                                      {2.1}

где max и min – максимальное и минимальное значения рабочих частот соответственно. Встроенная функция ceil(x) округляет результат в квадратных скобках до ближайшего минимального целого числа.

Точно так же введём функцию для расчёта