Логопериодические вибраторные антенны: Учебное пособие, страница 45

– стеклотекстолит марки СФ-2-35 – диэлектрическая проницаемость , тангенс угла электрических потерь ;

– стеклотекстолит марки СФТ-2-35 – диэлектрическая проницаемость , тангенс угла электрических потерь .

Видно, что тепловые потери в стеклотекстолите большие, примерно в 10 – 15 раз больше, чем в стандартных коаксиальных кабелях небольшого сечения. Но поскольку другого фольгированного материала в наличии обычно нет, следует проанализировать, как такие потери скажутся на характеристиках частично-печатной ЛПВА.

В нашем случае джоулевы потери в диэлектрике велики, поэтому потери за счёт конечной проводимости проводников ленточного фидера (потери в меди) учитывать не имеет смысла.

3.3. Расчёт параметров печатного распределительного фидера

Для анализа и проектирования ЛПВА в печатном и частично-печатном исполнении необходимо знать параметры ленточного двухпроводного распределительного фидера. В технической литературе обычно рассматривается несимметричная полосковая линия. Если между экраном и полосковым проводником в такой линии используется диэлектрик со значением , большим относительной диэлектрической проницаемости окружающего пространства, то такая линия называется микрополосковой линией.

Симметричный ленточный двухпроводный фидер можно рассматривать как две микрополосковые линии с общим экраном (рис. 3.13).

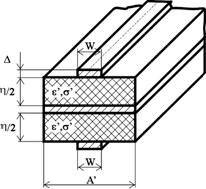
Рис. 3.13. Симметричный ленточный двухпроводный фидер

Волновое сопротивление такой симметричной линии равно удвоенному волновому сопротивлению одиночной микрополосковой линии, так как волновые сопротивления микрополосковых линий включены последовательно. Силовые линии электрического поля в такой линии везде перпендикулярны экрану (этого требуют граничные условия на поверхности с бесконечной проводимостью), следовательно, электрических токов на экране не наводится и его удаление не приведёт к изменению характеристик этой линии. Поэтому для описания характеристик ленточного двухпроводного распределительного фидера можно использовать выражения для микрополосковой линии. В этих выражениях необходимо увеличить в два раза волновое сопротивление и уменьшить в два раза толщину диэлектрика. В результате из выражения для волнового сопротивления микрополосковой линии [49] получаем формулу для волнового сопротивления ленточного двухпроводного фидера:

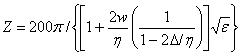,                        (3.9)

где w – ширина полоски ленточного фидера,  – толщина металла полоски ленточного фидера.

Из (3.9) находим ширину полоски ленточного фидера, реализующего требуемое волновое сопротивление,

.                                   (3.10)

Выражение (3.10) необходимо для расчётов, поэтому представим его в виде функции в Mathcad:

.                          {3.1}

Кроме геометрических размеров ленточного фидера при анализе ЛПВА необходимо знать величину замедления фазовой скорости и тепловые потери в фидере. Коэффициент распространения для симметричного ленточного фидера с диэлектрическим заполнением можно выразить аналогично (3.4):

.                                      (3.11)

В функции для расчёта параметров распределительного фидера {2.7} уже имеется коэффициент распространения свободного пространства k. Для учёта коэффициента замедления и тепловых потерь в ленточном симметричном фидере на основе (3.2) и (3.4) построим функции для их расчёта с учётом особенностей ленточного фидера. Вначале учтём толщину полоски распределительного фидера согласно (3.3):