Логопериодические вибраторные антенны: Учебное пособие, страница 22

Направление максимума излучения совпадает с направлением движения волны в распределительном фидере. Заканчивается распределительный фидер поглощающим резистором R_п с сопротивлением, равным волновому сопротивлению фидера.

Элементы связи (обычно резистивные) используются для расширения рабочего диапазона частот антенны, но одновременно они вносят значительные потери. В дециметровом диапазоне обычно нет необходимости в широком рабочем диапазоне частот, поэтому резистивные элементы связи можно исключить и тем самым уменьшить джоулевы потери.

Основные отличия при анализе АБВ заключаются в описании распределительного фидера. Для того, чтобы меньше изменять уже полученные расчётные соотношения, будем нумеровать вибраторы со стороны поглощающего резистора. Поскольку в этой антенне все расстояния между вибраторами одинаковые (), то выражение (1.2) для , с учётом поглощающего резистора, примет вид.

В свою очередь, изменится выражение (1.3): . Упростится и выражение (1.4) для : . В выражении (1.5) для соседних с диагональными элементов матрицы  и  изменится знак за счёт отсутствия инверсии фазы: .

Выражение для волнового сопротивления распределительного фидера получаем аналогично (1.13)

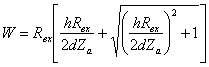.                                (1.47)

Для анализа характеристик в АБВ можно использовать как синусоидальное приближение, так и трёхчленный закон распределения токов.

Антенна Уда-Яги отличается от рассмотренных выше антенн, в первую очередь, тем, что в ней отсутствует распределительный фидер, питание подаётся к одному активному вибратору, а оставшиеся пассивные вибраторы связаны с активным вибратором только электромагнитно (рис. 1.11).

Рис. 1.11. Схема антенны Уда-Яги

Нумеровать вибраторы следует начинать с рефлектора. Для антенны Уда-Яги можно получить систему ИУ из (1.31), если учесть, что в правой части системы ИУ имеется только одно напряжение, подводимое к активному вибратору, и в антенне нет распределительного фидера. Примем синусоидальное приближение для распределений токов вдоль вибраторов антенны, подводимое напряжение примем равным 1В и из (1.31) получим систему линейных алгебраических уравнений (1.37) относительно токов в вибраторах антенны. Выражения для элементов матрицы и правой части системы в этом случае изменятся. Имеем

;           (1.48)

Поскольку входное напряжение принято равным одному вольту, то входное сопротивление антенны полностью определяется входным током активного вибратора:

, Ом.                                          (1.49)

С учётом перечисленных выше отличий антенны Уда-Яги от ЛПВА выражение для КНД можно получить из (1.46), разделив результат на квадрат модуля входного тока. Если принять во внимание (1.49), то выражение для КНД можно представить в двух вариантах:

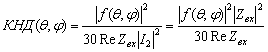.                           (1.50)

При использовании трёхчленного закона распределения токов (1.41) для антенны Уда-Яги применима система линейных алгебраических уравнений (1.37), в которой выражения для элементов матрицы и правой части системы имеют вид