Логопериодические вибраторные антенны: Учебное пособие, страница 15

.                           (1.15)

1.3. Интегральное уравнение Галлена для одиночного вибратора

Далее анализ ЛПВА следует проводить на основе системы ИУ Галлена. Вначале рассмотрим ИУ Галлена для тонкого симметричного электрического вибратора.

Задача об излучении электромагнитных волн вибраторными антеннами обычно решается в два этапа: на первом определяется распределение тока по вибраторам антенны, а на втором рассчитываются электрические характеристики по найденному распределению тока.

Распределение тока по антенне и векторы ЭМ поля, возбуждённого этим током, должны удовлетворять уравнениям Максвелла в комплексной форме:

,                       (1.16)

где  – комплексные амплитуды векторов напряжённостей электрического и магнитного полей,  – комплексная амплитуда плотности объёмного тока в вибраторе,  – угловая частота,  – комплексная диэлектрическая и магнитная проницаемости (абсолютные).

Определяя комплексную амплитуду электрического векторного потенциала  выражением , находим из (1.16) комплексную амплитуду вектора напряжённости электрического поля

,                                    (1.17)

Термин «комплексная амплитуда» далее опускаем для сокращения записи.

Электрический векторный потенциал удовлетворяет уравнению Гельмгольца [47, 50]

,

где  - рассматривается как плотность стороннего тока.

Рассмотрим симметричный электрический вибратор длины 2h (рис. 1.9).

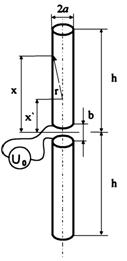
Рис. 1.9. Симметричный электрический вибратор

Ось x декартовой системы координат направлена вдоль оси вибратора, а начало её расположим в середине зазора. Длину зазора обозначим через b. Тогда решением уравнения Гельмгольца является [46, 47]

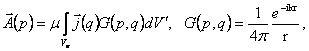                           (1.18)

где G – функция Грина неограниченного пространства,  - точка наблюдения ЭМ поля,  - точка интегрирования, расположенная в объёме  источника (вибратора),  - коэффициент распространения ЭМ поля в свободном пространстве, равный коэффициенту фазы,  - расстояние между точками p и q.

Будем предполагать, что плечи вибратора имеют идеальную проводимость, вибратор является тонким, т.е. , токами на концах вибратора пренебрегаем. При этом вектор плотности поверхностного электрического тока имеет только одну составляющую, направленную вдоль оси вибратора [46, 47, 50], т.е. . Тогда из (1.18) имеем

где S – поверхность плеч вибратора, по которой протекает поверхностный ток с плотностью (x), равной нулю на концах плеч вибратора,  - точка интегрирования на S.