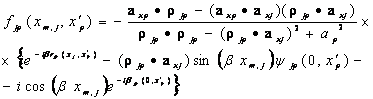 (5.26)
(5.26)
В результате получено ИУ для одиночного кусочно-линейного вибратора (5.20) с ядром, записанным в виде (5.21–5.26), которое подобно уравнению (1.40) и переходит в него, если принять количество сегментов s=1 (прямолинейный вибратор).
Основываясь на полученном ИУ, запишем его для ЛПВА. При этом положим возбуждающий ток равным 1А (рис. 5.1). Для системы связанных кусочно-линейных вибраторов нам неизвестны U0 в (5.20), для их определения воспользуемся (1.33-1.34), где Un=U0. В результате получаем
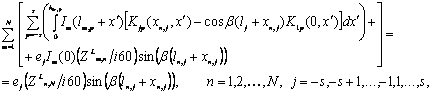
где ![]() – координаты точки наблюдения, находящейся на j-том
сегменте n-го вибратора,
– координаты точки наблюдения, находящейся на j-том
сегменте n-го вибратора, ![]() – это длина проводника от точки питания до начальной
точки n-го сегмента, а ZL=[YФ]-1
определяется из (1.2–1.5).
– это длина проводника от точки питания до начальной
точки n-го сегмента, а ZL=[YФ]-1
определяется из (1.2–1.5).
Заметим, что точка наблюдения xn,j и точка интегрирования x’ должны проходить всю длину кусочно-сегментного вибратора. Однако, с учетом того, что вибраторы в антенне симметричные, получаем, что токи на сегментах вибраторов, имеющих одинаковые номера, равны. Но токи на сегментах с отрицательными номерами направлены навстречу векторам axm,j, следовательно, количество членов суммы по p можно сократить в 2 раза и количество точек наблюдения xn,j также сокращается в 2 раза. Имеем:
 , (5.27)
, (5.27)
![]() , (5.28)
, (5.28)
где
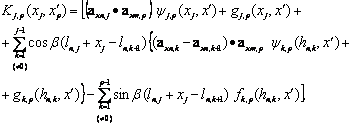 (5.29)
(5.29)
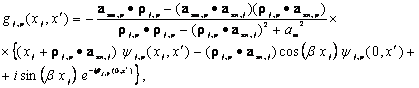 (5.30)
(5.30)
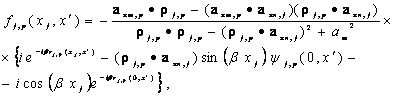 (5.31)
(5.31)
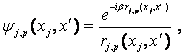
![]() , (5.32)
, (5.32)
![]() , (5.33)
, (5.33)
где (¹0) означает, что сумма равна нулю, если ее верхний индекс (j-1) равен нулю.
Численное решение системы ИУ (5.27) производилось методом согласования в точках путем разложения искомых распределений токов по вибраторам в ряды Фурье по Q синусоидальным гармоникам (число Q=x S, где x любое целое, кроме 0) и сведением системы ИУ к системе линейных алгебраических уравнений (СЛАУ):
![]()
в которой ![]() – искомые
коэффициенты разложения, а
– искомые
коэффициенты разложения, а
![]() . (5.34)
. (5.34)
Функция вида (5.34) выбрана из условия равенства тока на концах вибратора, она обеспечивает меньшие затраты машинного времени при решении задачи на ЭВМ по сравнению с функциями, приведенными в [64].
При условии, что (5.27) выполняется в дискретных
точках, где ![]() , причем j=1, при n £ x, j=2, при x < n £ 2bx, и т.д., n=1,2,…,Q,
, причем j=1, при n £ x, j=2, при x < n £ 2bx, и т.д., n=1,2,…,Q,
имеем СЛАУ 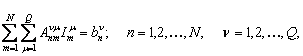
в которой ![]() , (5.35)
, (5.35)
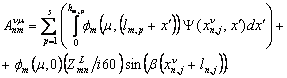 (5.36)
(5.36)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.