Логопериодические вибраторные антенны: Учебное пособие, страница 28

Теперь функцию для расчёта массива чисел первого члена правой части  (1.37б) можно получить в следующем виде

,         {2.26}

где h, h3 – массивы длин вибраторов  и , соответственно; l – массив расстояний ; c, c2, c3 – массивы ,  и , соответственно; s – массив ; ha – отношение высоты вибратора к радиусу; N – количество вибраторов.

Теперь можно разрабатывать функцию для расчёта токов. Учтём, что массив чисел  необходим только для расчёта токов, поэтому вычислять его следует в теле функции для расчёта токов, так как больше он нигде не нужен. Кроме того, в правой части (1.37б) имеются сомножители , которые также необходимо предварительно вычислить. Массив  необходим для расчёта входного сопротивления (1.46) и для построения графиков распределения тока вдоль антенны (1.36), поэтому введём функцию

.                   {2.27}

В результате получаем функцию для расчёта токов

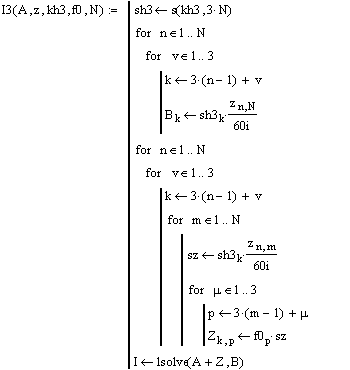,       {2.28}

где A – результат функции {2.26} – матрица первых членов правой части  (1.37б); z – матрица , результат функции {2.7}; kh – массив ; kh3 – массив  – результат функции {2.23}; f0 – массив  – результат функции {2.27}, N – количество вибраторов.

Первая строка вычисляет массив , следующие 4 строки – расчёт вектора правой части системы (1.37а), далее 8 строк – расчёт матрицы вторых членов правой части  (1.37б) и в последней строке окончательно формируется матрица системы  и решается система уравнений.

Функция {2.28} определяет составляющие токов в вибраторах. Для определения величины суммарных токов вибраторов в точках питания воспользуемся (1.36)

,            {2.29}

где I3 – массив гармоник токов – результат функции {2.28}; f0 – массив  – результат функции {2.27}, N – количество вибраторов.

Для определения входного сопротивления антенны используется функцию {2.16}, в которую подставляют токи, полученные в {2.29}. КСВ рассчитывается с помощью {2.17}.

Для расчета ДН одиночного вибратора построим функцию на основе (1.45). Выражение (1.45) содержит особенности для некоторых значений углов  и , что приводит к появлению пиков на графиках ДН. Строгий подход к этой проблеме требует отыскания этих особенностей, вычисления пределов и внесения изменений в функцию для расчёта ДН. В этом случае функция для расчёта ДН заметно усложнится. Однако большую часть этих пиков удаётся обойти, если выбрать дискретность изменения углов  и  дробной, например . ДН ЛПВА симметрична относительно оси антенны. Поэтому для устранения последнего пика заменим в теле функции угол  на  при .