Построим функцию для расчета матрицы
проводимостей распределительного фидера ![]() (выражения
(1.2а) – (1.5)) и преобразования матрицы
(выражения
(1.2а) – (1.5)) и преобразования матрицы ![]() в
матрицу
в
матрицу ![]()
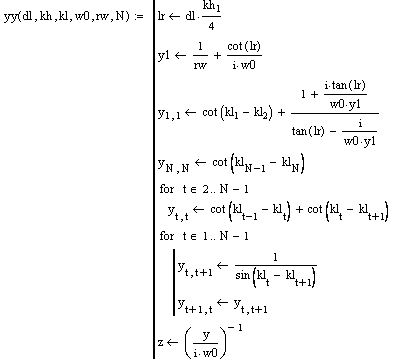 , {2.7}
, {2.7}
где dl – коэффициент, позволяющий изменять расстояние между первым вибратором и короткозамыкателем и численно устанавливать влияние этого расстояния на характеристики антенны; kh, kl – массивы электрических длин вибраторов и электрических расстояний от вершины антенны соответственно; w0 – волновое сопротивление распределительного фидера; rw – сопротивление поглощающего резистора; N – количество вибраторов.
В выражениях для
анализа характеристик ЛПВА часто используются значения ![]() и
и
![]() . Поэтому следует заранее один раз
вычислить массивы этих чисел и в дальнейшем использовать готовые значения:
. Поэтому следует заранее один раз
вычислить массивы этих чисел и в дальнейшем использовать готовые значения:
 , {2.8}
, {2.8}
 . {2.9}
. {2.9}
Элементы
матрицы системы линейных алгебраических уравнений и правая часть системы
описываются выражением (1.40). Составлять программы для их расчёта начнём с
подынтегрального выражения. Последнее состоит из произведения двух функций –
функции распределения тока (1.38) и ядра (1.31), причём ![]() –
знаменатель (1.38) вынесен за знак интеграла. В результате получаем
–
знаменатель (1.38) вынесен за знак интеграла. В результате получаем
![]() , {2.10}
, {2.10}
 , {2.11}
, {2.11}
где x – переменная
интегрирования; y – квадрат расстояния между m-ным и n-ным
вибраторами; kh – массив ![]() ; ch –
массив значений
; ch –
массив значений ![]() ; n, m –
номера вибраторов.
; n, m –
номера вибраторов.
Функция
{2.10} описывает закон распределения тока (без учёта знаменателя ![]() ), а функция {2.11} – ядро.
), а функция {2.11} – ядро.
Далее,
построим функцию для расчёта массива чисел первого члена правой части ![]() (1.40)
(1.40)
 {2.12}
{2.12}
Аргументы
функции {2.12} понятны из наименований (sh – массив
значений ![]() ).
).
Вычислять отдельно оставшиеся части выражений (1.40), на наш взгляд, не имеет смысла, удобнее это сделать в теле функции для расчёта токов:
 , {2.13}
, {2.13}
где A – результат
функции {2.12} – матрица первых членов правой части ![]() (1.40);
z – матрица
(1.40);
z – матрица ![]() , результат
функции {2.6}; sh – массив значений
, результат
функции {2.6}; sh – массив значений ![]() ; N –
количество вибраторов.
; N –
количество вибраторов.
В первых трёх строках
функции {2.13} рассчитывается матрица вторых членов правой части ![]() (1.40), в следующих двух строках
выделяется правая часть системы линейных алгебраических уравнений (1.39). В
последней строчке окончательно формируется матрица системы
(1.40), в следующих двух строках
выделяется правая часть системы линейных алгебраических уравнений (1.39). В
последней строчке окончательно формируется матрица системы ![]() и решается система уравнений.
и решается система уравнений.
После
нахождения токов в вибраторах основную часть расчётов характеристик ЛПВА можно
считать выполненной. Осталось построить графики распределения амплитуд и фаз
найденных токов по длине антенны и ДН в главных плоскостях, а также найти
численные значения входного сопротивления, КНД и КСВ на текущей частоте. В
связи с тем, что в Mathcad нет символа ![]() ,
а имеется только символ
,
а имеется только символ ![]() , то во всех
последующих функциях вместо символа
, то во всех
последующих функциях вместо символа ![]() используется
символ
используется
символ ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.