Логопериодические вибраторные антенны: Учебное пособие, страница 17

так как вне зазора .

Подставляя  и  в (1.21), интегрируя результат, учитывая 2-й закон Кирхгофа и обозначая через , напряжение источника сторонней ЭДС, получаем

,                         (1.22)

где  - характеристическое сопротивление среды, верхний знак берётся при , а нижний – при .

Из выражения (1.22) видно, что сторонний источник возбуждает на плечах вибратора две бегущие волны тока, одна из которых с волновым множителем  распространяется в направлении конца вибратора, где x = -h, а вторая с волновым множителем  - распространяется в направлении другого конца вибратора, где x = h. Коэффициенты С₁ и С₂ при волновых множителях учитывают обратные (отражённые от концов вибратора) волны тока. Наложение навстречу бегущих волн должно определять распределение тока по вибратору.

Подставим в левую часть равенства (1.22) значение  из (1.19) и умножим результат на . Имеем

.

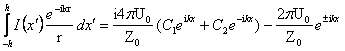Обозначим  - постоянные коэффициенты. Тогда можно упростить последнее выражение. Имеем

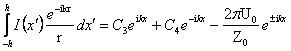.                     (1.23)

Правую часть (1.23) с помощью формулы Эйлера выразим через тригонометрические функции. Интегрирование в левой части равенства выполним раздельно по обоим плечам вибратора. Получаем

,                     (1.24)

где ,  - постоянные коэффициенты.

Определим ток  в точке при , где . Получаем из (1.24)

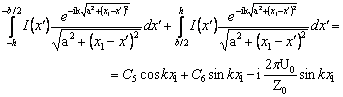                   (1.25)

Определим ток в симметричной точке при , где . Получаем из (1.24)

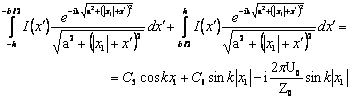
Выполним здесь замену переменных интегрирования по правилу  и учтём, что значение определённого интеграла не зависит от обозначения переменной интегрирования . Поэтому заменим  на  в результате. Получим

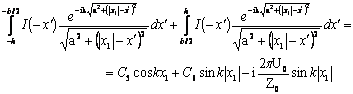       (1.26)

Сравнение (1.25) с (1.26) показывает, что условию равенства токов в симметричных точках вибратора, т.е. условию , (1.24) удовлетворяет только при . Таким образом, с учётом того, что Ом из (1.24) имеем

.

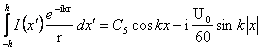Коэффициент  здесь можно исключить. Полагая , имеем