Логопериодические вибраторные антенны: Учебное пособие, страница 11

На самом деле в ЛПВА происходят более сложные процессы и энергия передаётся от вибратора к вибратору не только по распределительному фидеру, но и по пространству через поле излучения, однако, качественно картина работы сохраняется.

Между прочим, в самом принципе работы ЛПВА уже имеются основы для некоторого уменьшения габаритов. Во-первых, ЛПВА, как и любая антенна бегущей волны осевого излучения, несёт в себе некоторую сверхнаправленность, которая в идеальном случае увеличивает КНД примерно на 3 дБ. Во-вторых, за счёт того, что основная часть подводимой энергии излучается более короткими вибраторами, в большинстве случаев можно несколько укоротить самый длинный вибратор антенны. А так как все размеры антенны определяются размером самого длинного вибратора, то его укорочение приводит к заметному уменьшению габаритов всей антенны.

Будем предполагать, что распределительный фидер не участвует в излучении антенны. Это допущение позволяет при описании распределительного фидера пользоваться методами теории цепей, а для системы вибраторов применять хорошо развитые в настоящее время методы электродинамического анализа параллельных проводников с токами.

По Кэррелу ЛПВА представляет собой параллельное соединение двух многополюсников (рис. 1.3), один из которых описывает систему из N вибраторов (рис. 1.3а), связанных между собой через поле излучения, другой – распределительный фидер с расположенными на соответствующих расстояниях переменно-фазными отводами (рис. 1.3 б), представляющими собой клеммы, к которым подключаются излучатели.

а                                                              б                                   

в

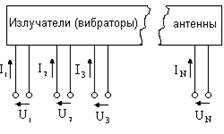
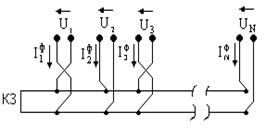
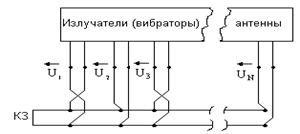
Рис. 1.3. Эквивалентная схема многополюсника фидера (а), эквивалентная схема многополюсника вибраторов (б), эквивалентная схема ЛПВА (в)

Обозначив матрицы проводимостей этих многополюсников соответственно через  и  и имея ввиду, что при параллельном включении матрицы проводимостей складываются, можно получить матричное уравнение относительно вектора напряжений на клеммах вибраторов . Такой подход к решению задачи применял Кэррел [5]. Для нас наибольший интерес представляет описание распределительного фидера с помощью матрицы .

Наиболее распространённой является так называемая переменно-фазная ЛПВА. В ней соединительные четырёхполюсники представляют собой отрезки двухпроводной линии с дополнительной инверсией фазы, что условно изображено на рис. 1.2,а в виде перекрещенных проводников.

1.2. Расчёт параметров распределительного фидера

Как следует из теории цепей, элементы матрицы  определяются путём короткого замыкания всех клемм распределительного фидера, кроме m-й клеммы, к которой подключается источник напряжения. В силу этого в данной матрице отличны от нуля лишь элементы ,  и , то есть диагональные и соседние с диагональными. Таким образом, матрица  без труда выражается через Y-параметры четырёхполюсников, образующих распределительный фидер. Для определения элемента  воспользуемся представленной на рис. 1.4 схемой.