Логопериодические вибраторные антенны: Учебное пособие, страница 14

Если рассматривать малый элемент как ёмкостную нагрузку, то ёмкость пропорциональна длине элемента, а расстояние до j-го элемента  пропорционально его длине. Тогда приближённо можно считать, что величина ёмкости на единицу длины распределительного фидера постоянна.

Таким образом, к обычной погонной ёмкости ненагруженного фидера добавляется величина сосредоточенной ёмкости, обусловленной элементами малой длины.

Рассмотрим приближённую формулу для определения входного сопротивления вибратора

,                                  (1.6)

где  – среднее значение волнового сопротивления вибратора (в классической ЛПВА предполагается, что отношение  – величина постоянная)

.                                                (1.7)

Для вибраторов малой длины  равен коэффициенту фазы в свободном пространстве. Заменяя котангенс его приближённым значением  для -го вибратора при , получим для ёмкости -го вибратора

,                                                 (1.8)

где учтено, что , ,  – электрическая и магнитная постоянные,  – скорость света в вакууме,  – угловая частота. Вводя среднее расстояние до -го вибратора

,                                    (1.9)

получим выражение для средней погонной ёмкости

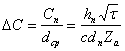,                                  (1.10)

или, учитывая, что , имеем

.                                       (1.11)

Так как волновое сопротивление двухпроводной линии , где  – погонные индуктивность и ёмкость длинной линии, и для линии с воздушным заполнением скорость света выражается через параметры линии как , то для входного сопротивления линии, нагруженной элементами малой длины, получим  или

,                                            (1.12)

где .

Из (1.12) найдём выражение для волнового сопротивления фидера

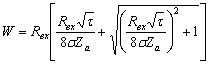.                                (1.13)

Волновое сопротивление двухпроводной линии определяется следующим выражением [46]

,                                    (1.14)

где и  – расстояния между центрами проводников и диаметры проводников, соответственно.

Из (1.14) получаем выражение для расстояний между центрами проводников по заданному волновому сопротивлению и диаметрам проводников