Логопериодические вибраторные антенны: Учебное пособие, страница 32

Параметр  выбираем по номограмме (рис. 2.1) – . Для упрощения выкладок отношение высоты вибратора к его радиусу будем считать постоянным и примем .

Рассматриваемые примеры расчётов приводятся для трёхчленного закона распределения токов, сравнение с синусоидальным приближением будет отмечаться.

Ввод исходных данных является первой строкой программы

.

Далее рассчитываем необходимое количество вибраторов N и «оптимальное»

.

В следующей строке значения N и  присваиваются снова

.

Эта строка вставлена для того, чтобы в дальнейшем параметры N и  можно было корректировать (изменять) в зависимости от получаемых результатов.

Осталось ввести ещё 4 переменных (параметра) – частотный коэффициент F, корректирующий множитель для волнового сопротивления распределительного фидера kw, корректирующий множитель dl, позволяющий изменять расстояние между первым вибратором и короткозамыкателем, и поглощающий резистор rw. По правилам Mathcad всем обычным (локальным) переменным необходимо присваивать значения до их дальнейшего использования. Кроме локальных переменных в Mathcad есть глобальные переменные, которые могут находиться в любом месте программы, но вычисляются в первую очередь. В нашем случае удобно сделать параметры F, kw, dl и rw глобальными переменными. Начальное значение F, kw и dl равно единице, а начальное значение rw равно 10⁸. Применительно к частотному коэффициенту F это означает, что расчёт производится для начальной частоты 470 МГц и что высота первого вибратора равна .

Следующий фрагмент программы рассчитывает электрические геометрические размеры антенны, волновое сопротивление распределительного фидера, массивы часто используемых чисел, матрицу  – параметров распределительного фидера, матрицу системы уравнений, вектор гармоник токов в вибраторах и вектор токов вибраторов в точках питания

.

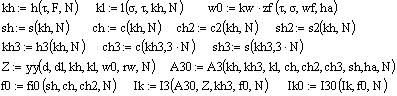Далее формируются массивы модулей и аргументов токов в точках питания, находится максимальный ток в антенне, определяется Z_вх, максимум ДН, КСВ и КНД. В последней строке задаются пределы изменения и шаг углов  и  для вывода ДН.

.

Рассмотрим графики распределения токов вдоль антенны на нижней граничной частоте (F0 = 1). Выведем значения Z_вх, КНД и КСВ на текущей частоте F = 1. Определим значение F на верхней граничной частоте (Fm), рассчитаем коэффициент пересчёта электрических размеров в линейные и выведем длину антенны и значение Fm:

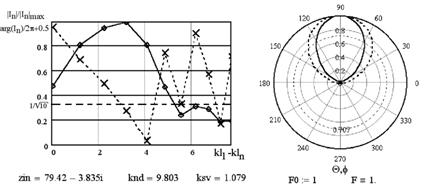
Рис. 2.2. Графики распределения токов и ДН на нижней граничной частоте

.

Получены графики распределений амплитуд (сплошная линия) и фаз (штриховая линия) токов по длине антенны, ДН в главных плоскостях, рассчитано волновое сопротивление распределительного фидера, Z_вх антенны, КНД и КСВ. В последней строке определена длина антенны как расстояние между первым и последним вибраторами.

На графике распределений токов видна активная область из длинных вибраторов. Амплитуда тока в первом вибраторе сравнительно небольшая, чуть больше уровня –10 дБ (уровню –10дБ в линейном масштабе соответствует уровень , который изображён на рис. 2.2 штриховой линией).