Логопериодические вибраторные антенны: Учебное пособие, страница 60

Основываясь на характеристике направленности для одиночного кусочно-линейного вибратора [64], запишем [36] для системы вибраторов

,                            (5.37)

где

,

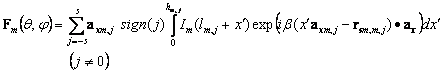a_r – нормированный радиус-вектор, проведенный из начала координат к точке наблюдения поля, а M_m – вектор, проведенный из начала координат в точку питания m-го вибратора, символ sign(j) означает “знак j”, и равен +1 или -1 в зависимости от знака номера j.

По коэффициентам разложений токов  находим входное сопротивление ЛПВА

.

КНД антенны определяем по формуле (1.46), подставив в нее вместо значение  из (5.37).

Используя приведенную выше методику, возможно рассчитывать не только ЛПВА с вибраторами любой конфигурации и любым количеством сегментов (ограничение имеется только на объем памяти ЭВМ и быстродействие последней), но и другие решетки таких вибраторов (например, Уда-Яги, антенны бегущей волны, несимметричные ЛПВА). Необходимо при этом “правильно” задать возбуждающие напряжения вибраторов решеток.

На основе приведенных выше формул была разработана программа на языке Borland C++ под операционную систему Windows 9x, разработка программы на языке Mathcad не имеет смысла из-за громоздкости выражений и значительных затрат машинного времени на расчеты даже при использовании современных персональных компьютеров.

5.3. Логопериодические вибраторные антенны с V-вибраторами

Рассмотрим систему из двух "связанных" V-вибраторов, расположенных в свободном пространстве (рис. 5.2). Упростим для них общие выражения ядра интегрального уравнения. Для этого выразим все необходимые векторы в декартовой системе координат с учетом расположения вибраторов на плоскости. Вибраторы находятся в плоскости y0z.

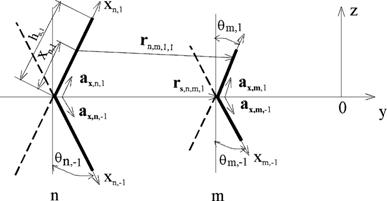
Рис. 5.2. Система связанных V-вибраторов

.

Необходимо упростить выражения для ядер K_n,m,1,1, K_n,m,1,-1 в (5.28–5.33).

Приводя подобные и упрощая, получаем следующие выражения для расчета параметров двух связанных V-вибраторов в виде:

, (5.37)

где введены обозначения:

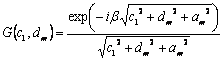,                                       (5.38)

где с₁, d_m – переменные функции (5.38),

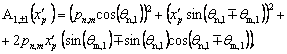                       (5.39)

,                              (5.40)

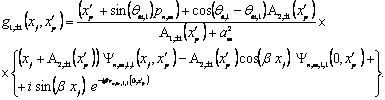        (5.41)

Исследуем численно, как повлияет изменение угла наклона вибраторов q_m,1 = q на частотные характеристики ЛПВА. Влияние угла наклона вибраторов V-антенны с геометрическими размерами, определяемыми следующими величинами: t=0,956, s=0,1315, N=9, f_min=937,5 МГц, W=51,28 Ом, длина короткозамыкателя за первым вибратором равна 0,1l_min, h/a=46, на зависимость КНД, КСВ в фидере антенны с волновым сопротивлением 50 Ом можно определить по результатам расчетов, приведенным на рис. 5.3.