Логопериодические вибраторные антенны: Учебное пособие, страница 58

,                         (5.6)

,                   (5.7)

где

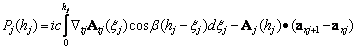,     (5.8)

,                       (5.9)

где символ обозначает скалярное произведение векторов, а в (5.8) учтен переход из системы координат j+1-го вибратора в систему координат j-го вибратора.

Используя рекуррентные соотношения (5.6) и (5.7), выразим постоянные интегрирования B_j и C_j через B₁ и C₁

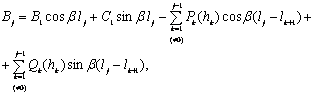                           (5.10)

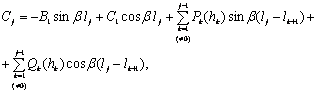                (5.11)

где l_j – длина проводника от точки питания до начальной точки j-го сегмента:

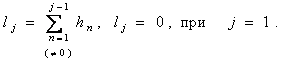               (5.12)

Подставив (5.10) и (5.11) в (5.3), запишем осевую компоненту векторного потенциала:

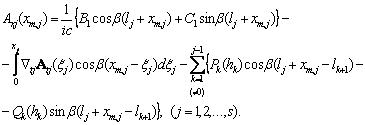             (5.13)

В другой области, где -s £ j £ -1, векторные потенциалы определяются аналогично:

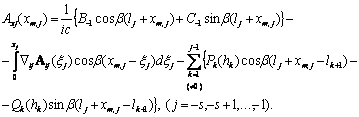     (5.14)

Константы B₁, C₁, B_-1, и C_-1 определим из граничных условий – (5.5,e) и (5.5,f), подставив в них (5.3) и (5.4). Получаем

,    .                              (5.15)

С другой стороны, векторные потенциалы токов, протекающих на секторах, (5.13) и (5.14) могут быть выражены через интеграл:

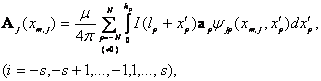               (5.16)

где

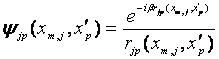,                              (5.17)

и

,             (5.18)

а

.                                         (5.19)

Подставив (5.16) и граничные условия (5.15) в (5.13), получаем ИУ для тока кусочно-линейного вибратора

где появилась новая постоянная В, которую возможно определить, если учесть, что при нахождении точки наблюдения x_m,j в начале первого и минус первого сегментов (j=1,-1), l_j +x_m,j = 0. Подставив это значение в ИУ и приведя подобные, окончательно получим:

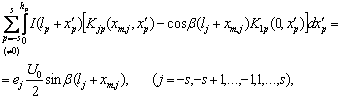                    (5.20)

где ядро K_jp (x_j, x^’_p) определено как

            (5.21)

,                           (5.22)

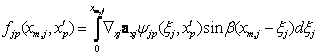,                        (5.23)

.                                                (5.24)

Производя интегрирование по частям в (5.22) и (5.23), приводя подобные, и заменяя переменные, преобразуем интегралы к виду, при котором исключено дифференцирование. В результате (5.22) и (5.23) примут вид

             (5.25)