![]() (1.37)
(1.37)
Правая часть системы
![]() (1.37а)
(1.37а)
а элементы матрицы определяются выражением
 , (1.37б)
, (1.37б)
в котором интегралы в свою очередь определяются численными методами.
Точность получаемого численного решения (а также трудоёмкость расчётов) в основном определяется выбором системы базисных функций (1.36). Как отмечалось выше, будем рассматривать два варианта системы базисных функций – синусоидальное распределение тока по вибратору и трёхчленное представление закона распределения тока, известное как гармоники Кинга.
Синусоидальное
распределение тока считается в случае тонких вибраторов справедливым при длинах
вибратора, не превышающих ![]() . В то же время в ЛПВА, предназначенной для работы в
широкой полосе частот, могут присутствовать и гораздо более длинные вибраторы.
Однако, как показано в [11], для антенн с КНД
. В то же время в ЛПВА, предназначенной для работы в
широкой полосе частот, могут присутствовать и гораздо более длинные вибраторы.
Однако, как показано в [11], для антенн с КНД![]() 7дБ
точность расчёта основных параметров (таких как диаграмма направленности,
входной импеданс и КНД) с учётом только синусоидального распределения
оказывается достаточной. Это обстоятельство можно объяснить тем, что в ЛПВА на
любой рабочей частоте активными являются вибраторы длиной не более
7дБ
точность расчёта основных параметров (таких как диаграмма направленности,
входной импеданс и КНД) с учётом только синусоидального распределения
оказывается достаточной. Это обстоятельство можно объяснить тем, что в ЛПВА на
любой рабочей частоте активными являются вибраторы длиной не более ![]() , распределение тока в которых хорошо
описывается синусоидальным приближением.
, распределение тока в которых хорошо
описывается синусоидальным приближением.
Возможны случаи, когда приближённый метод может привести к значительному завышению КНД по сравнению с истинным значением. Это имеет место для тех антенн, в которых по каким-либо причинам возбуждаются электрически длинные вибраторы. Например, для сжатых ЛПВА с большим углом при вершине возможно «просачивание» энергии по распределительному фидеру за активную область, вследствие чего происходит паразитное возбуждение длинных вибраторов. Аналогичное явление наблюдается в случае ЛПВА, состоящей из чрезмерно тонких вибраторов.
Синусоидальный закон распределения описывается следующим выражением
![]() , (1.38)
, (1.38)
где ![]() –
ток в середине m-го вибратора.
–
ток в середине m-го вибратора.
Система линейных алгебраических уравнений (1.37) в этом случае упрощается и имеет вид
![]() (1.39)
(1.39)
Упрощаются также выражения для элементов матрицы и правой части системы:
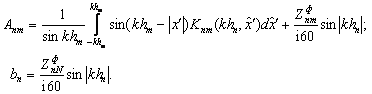 (1.40)
(1.40)
Для
нахождения тока в вибраторах при синусоидальном приближении необходимо задать
размеры антенны, найти параметры распределительного фидера (получить матрицу ![]() – параметров и преобразовать её в
матрицу
– параметров и преобразовать её в
матрицу ![]() – параметров) и с помощью выражений
(1.38) – (1.40) определить эти токи.
– параметров) и с помощью выражений
(1.38) – (1.40) определить эти токи.
Более точное решение [11] получается при использовании в разложении (1.36) следующих трёх функций, предложенных Кингом:
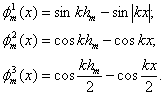 (1.41)
(1.41)
Как известно из курса антенн форма диаграммы направленности полностью определяет важнейшую энергетическую характеристику антенны – КНД. Воспользуемся следующим выражением для КНД [46]:
![]() ,
,
где ![]() - квадрат модуля полного вектора
напряжённости электрического поля в заданном направлении
- квадрат модуля полного вектора
напряжённости электрического поля в заданном направлении ![]() ,
, ![]() -
усреднённое по полному телесному углу значение квадрата модуля полного вектора
напряжённости электрического поля.
-
усреднённое по полному телесному углу значение квадрата модуля полного вектора
напряжённости электрического поля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.